Algèbre linéaire et
vecteurs
Algèbre linéaire
Exercices
Plan dans l'espace
Droite dans l'espace
|
Mathématiques 3: Algèbre linéaire
Les matrices
Rang d'une matrice
1. Définition
Le rang r d'une matrice A d'ordre (m,n) est inférieur ou égal à m et à n.
On peut ecrire rg (A) = r ≤ m ou n.
Le rang d’une matrice de dimension quelconque est l'ordre de la plus
grande sous-matrice carrée régulière que l'on peut extraire de cette
matrice.
Si une matrice a plus de lignes que de colonnes, alors le rang de cette matrice est au plus égal au nombre de colonnes.
Les TE (transformations élémentaires sur les lignes et sur les colonnes ne changent pas le rang d'une matrice.
Le rang d'une matrice est égal au nombre des lignes
de sa matrice escalier.
Le rang d'une matrice régulière est égale à son ordre.
2. Exemples:
Exemple 1:
|
A = |
 |
3 | - 2 | 4 |
 |
| 5 | 7 | - 3 |
| 1 | 1 | - 1 |
|
Le determinant de cette matrice est égal à - 24. A est donc
un matrice régulière. Son rang est égal à son ordre = 3
rang (A) = 3
Exemple 2:
|
B = |
 |
3 | - 2 | 4 |
 |
| 5 | 7 | - 3 |
|
Cette matrice d'ordre 2 x 3 n'est pas une matrice carrée.
La plus grande sous-matrice carrée est :
|
Bo = |
 |
3 | - 2 |
 |
| 5 | 7 |
|
de déterminant non nul. Son ordre est égal à 2.
Le rang de la matrice B est égal à = 2.
rang (B) = 2
Exemple 3:

Exemple 4:

Exemple 5:

Exemple 6:

Exemple 7:
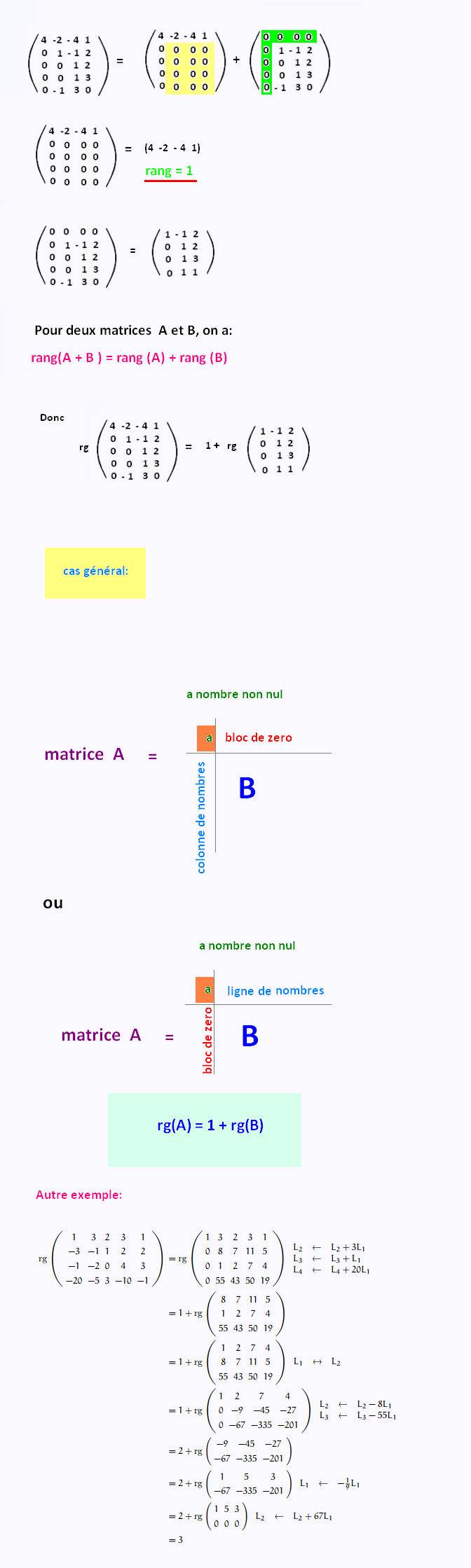
|
|