Mathematics
Conics
Hyperbola

Hyperbola:

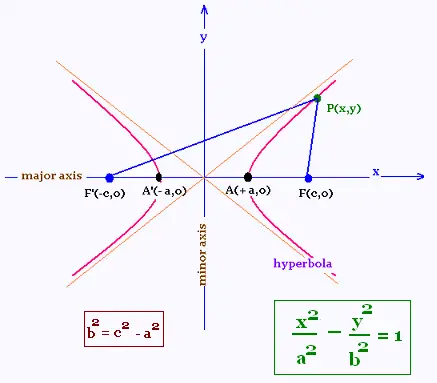
A hyperbola is defined as:


|dist (P,F) - dist(P,F')| = 2a

P is any point on the curve. F and F' are the two focii of the hyperbola; and "dist" is the distance between the two related points.

First, we will consider:

dist (P,F) < dist(P,F'), and b² = c² - a²

Let's then express the above equation:
|sqrt [(c - x)² + (0 - y)² ] - [(- c - x)² + (0 - y)²]^1/2| = 2a

Since dist (P,F) < dist(P,F'), or dist (P,F) - dist(P,F') < 0, and "a" is positive; the above equation is rewritten as:
dist (P,F) - dist(P,F') = - 2a, therefore:
[(c - x)² + y² ]^1/2 - [(- c - x)² + y² ]^1/2 = - 2a

[c² - 2cx + x² + y²]^1/2 = - 2a + [c² + 2cx + x² + y²]^1/2

c² - 2cx + x² + y² = 4a² - 4a [c² + 2cx + x² + y²]^1/2 + c² + 2cx + x² + y²

- 4cx = 4a² - 4a [c² + 2cx + x² + y²]^1/2

- cx = a² - a [c² + 2cx + x² + y²]^1/2

c²x² + 2cxa² + a⁴ = a² [c² + 2cx + x² + y²]<

[c² - a²]x² + a²[a² - c²] = a² y²

b²x² - a²b² = a² y²

b²x² - a² y² = a²b²

Then:

x²/a² - y²/b² = 1

x²/a² - y²/b² = 1

With: b² = c² - a²

That is the equation of an hyperbola.