Astronomie:
Compléments de Mathématiques
L'ellipse en coordonnées catrésiennes et
coordonnées polaires
1. Construction d'une l'ellipse
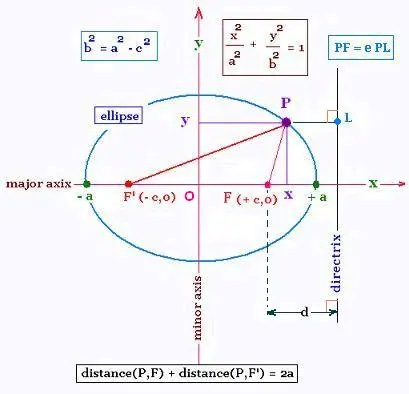
Une ellipse est un lieu géométrique défini par
dist (P,F) + dist(P,F') = 2a
P est un point sur la courbe.
F and F' sont les deux foyers de l'ellipse. Un foyer
est le centre de force d'une force centrale.
dist désigne la distance entre deux points considérés.
La distance focale c est la distance entre le centre
de l’ellipse O et un des foyers.
2. L'ellipse coordonnées cartésiennes
Partons de l'équation de définition ci-dessus
pour trouver l'expression cartésienne de l'ellipse.
√[(c - x)2 + (0 - y)2 ] +
[(- c - x)2 + (0 - y)2]1/2 = 2a
[(c - x)2 + y2 ]1/2 +
[(- c - x)2 + y2 ]1/2 = 2a
[c2 - 2cx + x2 + y2]1/2
= 2a - [c2 + 2cx + x2 + y2]1/2
c2 - 2cx + x2 + y2
=
4a2 - 4a [c2 + 2cx + x2 + y2]1/2 +
c2 + 2cx + x2 + y2
a [c2 + 2cx + x2 + y2]1/2
= a2 + cx
a2 [c2 + 2cx + x2 + y2]
= a4 + 2cx a2 + c2x2
a2 [c2 + x2 + y2]
= a4 + c2x2
a2 [ x2 + y2] - c2x2
= a2[a2 - c2]
x2[a2 - c2] + a2 y2]
= a2[a2 - c2]
x2 b2 + a2 y2
= a2b2
Donc:
x2/ a2 + y2/ b2 = 1
C'est l'équation d'une ellipse en coordonnées cartésiennes.
2. L'ellipse coordonnées polaires
2.1. L'excentricité de l'ellipse
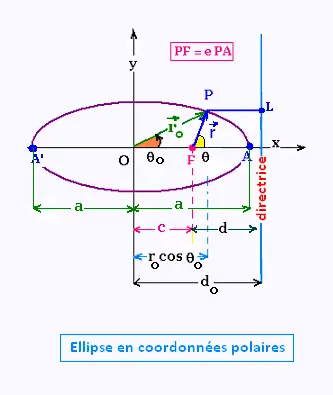
L' excentricité "e" d'une conique est défini pa
le rapport:
e = dist(P,F)/dist(P,L)
Appliqué au point P = A, et au puis au point P = A',
donne:
e = dist(A, F)/dist(A,L)
e = (a - c)/(do - a) (1)
e = dist(A',F)/dist(A',L)
e = (a + c)/(do + a) (2)
Additionnons(1) avec (2), on obtient
edo - ea = a - c
edo + ea = a + c
2edo = 2a. Donc e = a/do
e = a/do
Soustrayons (2) de (1), on obtient :
- 2 ea = - 2c.
Donc
e = c/a
e = c/a = a/do
avec:
0 < e < 1
Nous avons aussi
d = do - c = a/e - ae = a( 1/e - e) =
(a/e)(1 - e2). D'òu:
ed = e(a/e)(1 - e2) = a(1 - e2)
p = ed = a(1 - e2)
2.2. L'équation polaire d'une ellipse
La loi d'Al-Kashi (loi des cosinus) donne:
PF2 = ro2 + c2 - 2roc cosθo
Nous avons:
PL = do - ro cosθo
dist(P,F) = e dist(P,L), donne :
√[ro2 + c2 - 2ro c cosθo] = e(do - ro cosθo)
[ro2 + c2 - 2ro c cosθo]1/2 = e(do - ro cosθo)
ro2 + c2 - 2ro c cosθ o = e2do2 +
e2 ro2 cos2 θo - 2 rodoe2 cosθo
ro2[1 - e2 cos2 θo] + 2ro cosθo [ doe2 - c] + c2
- e2do2 = 0
Or edo = a, ae = c, et b2 = a2 - c2 Donc:
ro2[1 - e2 cos2θo] = b2
ro = b/[1 - e2 cos2θo]1/2
ro = b/[1 - e2 cos2θo]1/2 =
[(a2 - c2)/(1 - e2 cos2 θo)]1/2
Pour simplifier, on prend Le foyer F comme origine des
coordonnées. Nous avons donc:
c = 0 et
d = do
r = dist(F,P) = e dist(P,L)
dist(P,L) = d - r cos θ.
Donc
r = e [d - r cos θ ]
r [1 + e cos θ] = ed
r = e d /[1 + e cos θ ]
L'équation d'une ellipse en coordonnées
polaires est donc:
r = p/(1 + e cosθ) =
a(1 - e2)/(1 + e cosθ)
Avec
p = ed = a(1 - e2)
e est l'excentricité de l'ellipse et d est la distance entre
la directrice est le foyer de l'ellipse.
2.3. Résumé: paramètres d'une ellipse
Excentricité \(e\)
\(e = \dfrac{c}{a}\).
Demi grand-axe \(a\)
\(a = \dfrac{p}{1-e^2}\)
Demi petit-axe \(b\)
\( b^2 = a^2 - c^2 = a^2 - (a e)^2 = a^2 - a^2e^2 = \;
a^(1 - e^2) = ap
\\
b = \sqrt{ap}
\)
Distance focale \(c\)
\(c = ae = \dfrac{p\,e}{1-e^2}\)
Demi-petit axe \(b\)
Noua avons: \(a^2 = b^2 + c^2\)
\(b^2 = a^2 - c^2 = \dfrac{p^2}{(1-e^2)^2} - \dfrac{p^2e^2}{(1-e^2)^2} = \dfrac{p^2}{1-e^2}\)
D’où :
\(b = \dfrac{p}{\sqrt{1-e^2}} = a\,\sqrt{1-e^2} = \sqrt{ap}\)
|