Astronomie:
Compléments de Mathématiques
Loi des aires et énegie mécanique

1.Moment cinétique d'un point matériel
soumis à une force centrale conservative

1.1. Mouvement d'un point soumis à une force centrale

le moment cinétique, par rapport à un point O, d'un point matériel M de masse m, se déplçant à une vitesse $\vec{\mathbf{v(M)}}$ et soumis à une force $\vec{\mathbf{F}}$ est défini par:

$\overrightarrow{L_O}(M) = \overrightarrow{OM} \times m\vec{\mathbf{v(M)}}$


Le théorème du moment cinétique par rapport à O, dans le référentiel galiléen (O, $\vec{\mathbf{e_x}}, \vec{\mathbf{e_y}}, \vec{\mathbf{e_z}}$ ) s'ecrit:

$\frac{d\overrightarrow{L_O}(M)}{dt} = \overrightarrow{OM}(\vec{\mathbf{F}}) = \overrightarrow{OM} \times m \frac{\vec{\mathbf{dv(M)}}}{dt} = \overrightarrow{OM} \times \vec{\mathbf{F}}$

La force étant centrale , on ecrit donc:

$\frac{d\overrightarrow{L_O}(M)}{dt} = r \;\vec{\mathbf{u_r}} \times F(r) \; \vec{\mathbf{u_r}} = r \; F(r)\; \vec{\mathbf{u_r}} \times \vec{\mathbf{u_r}} = r\; F(r) \;. 0 = 0.$


Le point M n'étant sounis qu’à une force centrale rend son moment cinétique constant. Ainsi

$\frac{d\overrightarrow{L_O}(M)}{dt} = 0$

traduit :

$\overrightarrow{L_O}(M) = \overrightarrow{OM} \times m \; \vec{\mathbf{v(M)}} = \overrightarrow{cst} \;.$

Ainsi, le point M se déplace constamment sur un plan défini par les vecteurs $\overrightarrow{OM} \; et \;\vec{\mathbf{v}}(M).$
Ce plan est perpendiculaire à $\overrightarrow{L_O}(M),$ le moment cinétique du point M.


Le mouvement d'un point soumis
à une force centrale est plan.

1.2. Loi des aires

La deuxième conséquence de la constance du moment cinétique d'un point soumis à une forec centrale est la loi des aires .

En coordonnées cylindriques, le vecteur moment cinétique du point M s'ecrit :

$\bf{ \overrightarrow{L_O}(M) = \overrightarrow{OM} \times m \; \vec{\mathbf{v(M)}} = m \;r\; \vec{\mathbf{e_r}} \;\times \; (\frac{dr}{dt} \; \vec{\mathbf{e_r}} + r \; \frac{d\theta}{dt}\vec{\mathbf{e_\theta}}) = \\ m\; r^2 \; \frac{d\theta}{dt} \; \vec{\mathbf{e_z}}= \overrightarrow{cst} \;}.$

On ecrit:

$\overrightarrow{L_O}(M) = m \; C \; \vec{\mathbf{e_z}},$ avec: $\Large{ C = r^2 \frac{d\theta}{dt} }$

L’aire balayée par le rayon vecteur $\overrightarrow{OM}$ pendant un temps dt s'ecrit:



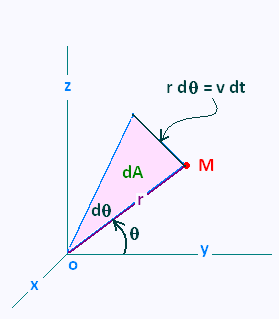
dA = (1/2) OM x v(M) dt = (1/2) r x r dθ =
(1/2) r x r (dθ/dt) dt = (1/2) r² (dθ/dt) dt =
(C/2) dt. D'où:

dA/dt = C/2

Ainsi, La vitesse aréolaire ou la vitesse de balayage de l'air A est

A = (C/2) t + cst.

Laire balayée par le rayon vecteur $\overrightarrow{OM}$ est proportionnelle au temps. C’est la loi des aires.

2. Énrgie mécanique du point matériel M

Lorsqu'une force appliqué à point est centrale, cette force est conservative. Ainsi son érergie mécanique est constante tout au long de son mouvement.

Le théorème de l'énegie cinétique s'énonce :

La différence entre l'énergie cinétique finale et énergie cinétique initiale d'un point mobile est égale au travail effectué par la force nette sur le mobile.

Du momemnt où l'énergie mécanique est constante, the théorème de l'énergie cinétique s'énonce également :

La différence entre l'énergie potentielle finale et énergie potentielle initiale d'un point mobile est égale à l'inverse du travail effectué par le force nette sur le mobile.

$\Large{ \Delta E_C = W(\vec{\mathbf{F}}) \;\; ou \;\; \Delta E_P = - W(\vec{\mathbf{F}}) }$

La force appliquée au point M est concervative.

$\Large{\color{brown}{ F(r) = - \frac{dE_p}{dr} = \frac{K}{r^2}} }\;$

Ainsi pour un travail d'une position quelconque A vers une position quelconque B du pont M, on a:

$\large{ W(\vec{\mathbf{F}}) = - \; \Delta E_P = E_p(A) - E_p(B). \\ } \\ \\ \bf{\color{green}{ \begin{equation} W_{AB}(\overrightarrow{F}) = \int_A^B F(r) dr = \int_A^B \dfrac{K}{r^2}\,dr = \left[-\dfrac{K}{r}\right]_A^B = E_P(A) - E_P(B) \end{equation} } }$ On trouve donc

$\begin{equation}E_C(A) + E_P(A) = E_C(B) + E_P(B) = \mathrm{cste}\end{equation}$

C'est à dire

$\begin{equation}E_\mathrm{M} = E_C + E_P = \mathrm{cste}\end{equation}$

Qui traduit que l'énergie mécanique du point M est constante. Par conséquent, elle reste et est égale à tout instant à sa valeur initiale.

Ainsi les conditions initiles permettent de déterminer sa valeur.

$\Large{ \begin{equation} E_P(r) = \dfrac{K}{r} + \mathrm{cste}. \\ E_\mathrm{C} = \frac{1}{2}mv^2 = \frac{1}{2}m(\overset{\centerdot}{r}\,^2+r^2\overset{\centerdot}{\theta}\,^2) \\ \\ C = r^2 \frac{d\theta}{dt} = r^2 \overset{\centerdot}{\theta} \\ \\ E_\mathrm{C} = \frac{1}{2}m\overset{\centerdot}{r}^2 +\dfrac{mC^2}{2\,r^2} \\ \\ E_\mathrm{M} = E_\mathrm{C} + E_\mathrm{P} \\ \\ \; \\ \color{blue}{E_\mathrm{M} = \frac{1}{2}m\overset{\centerdot}{r}^2 +\dfrac{mC^2}{2\,r^2} + \dfrac{K}{r} + \mathrm{cste}} \end{equation} }$


L'énergie mécanique du point M s'exprime en fonction de l’unique variable r.

$E_{\mathrm{Peff}}(r) = E_P(r) + \dfrac{mC^2}{2\,r^2}$ est appelée énergie potentielle effective.