Exercices
Mathématiques
Baccalauréat 2
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Math - Fonction implicite
Analyse
Suite implicite
Suite de fonctions
Rappels:
1. Théorème du sandwich:
En analyse, le théorème des gendarmes, également appelé théorème
d'encadrement ou théorème du sandwich, s'ecrit:
f, g et h trois fonctions d'un intervalle I vers R.
"a" un élement de I, et "l" un élément de R.
Si ∀ x ∈ I: f(x) ≤ g(x) ≤ h(x) et si
lim f(x) = lim h(x) = l
x → a
, alors g(x) converge en a, et
lim g(x) = l
x → a
2. Théorème de Bolzano:
Pour toute application f continue de [a, b] sur R, si
f(a) . f(b) ≤ 0, alors il existe au moins un réel
c ∈ [a,b] tel que f(c) = 0.
3. Raisonnement par l'absurde:
Le raisonnement par l'absurde est une technique logique qui permet de prouver qu'une affirmation est vraie en montrant que son contraire est faux.
4. Théorème de convergence monotone:
Si une suite est croissante et majorée , alors elle est convergente. De façon similaire,
Si une suite est décroissante et minorée , alors elle est convergente aussi.
Exemple:
On considère une suite de fonction fn de R+ vers R, telle que :
fn(x) = 3xn - x - 1 , n ∈ N*
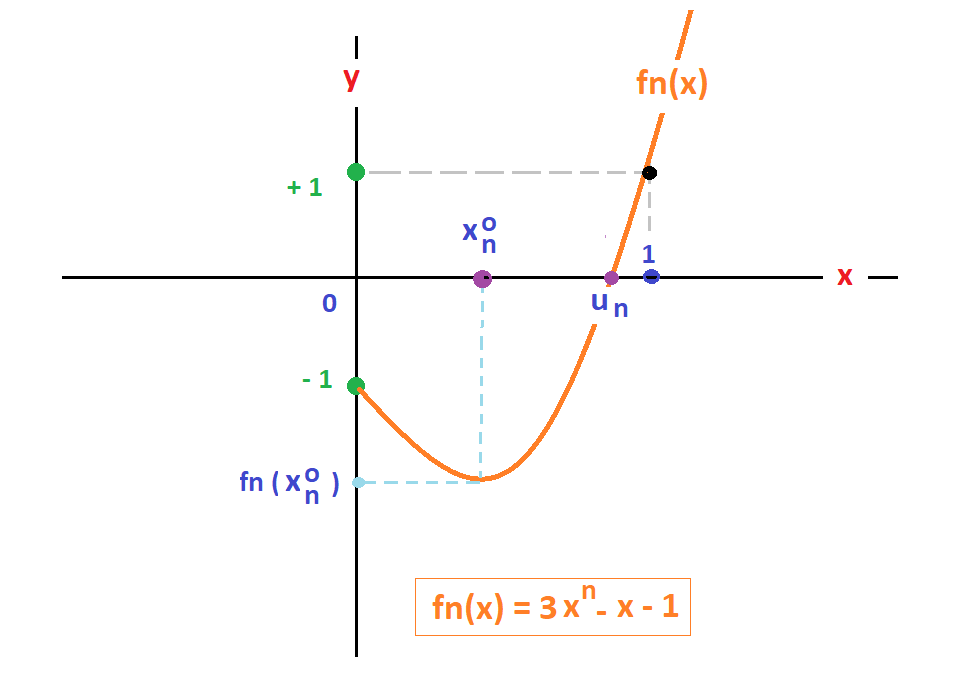
0. Allure de la fonction fn (x) sur R+:
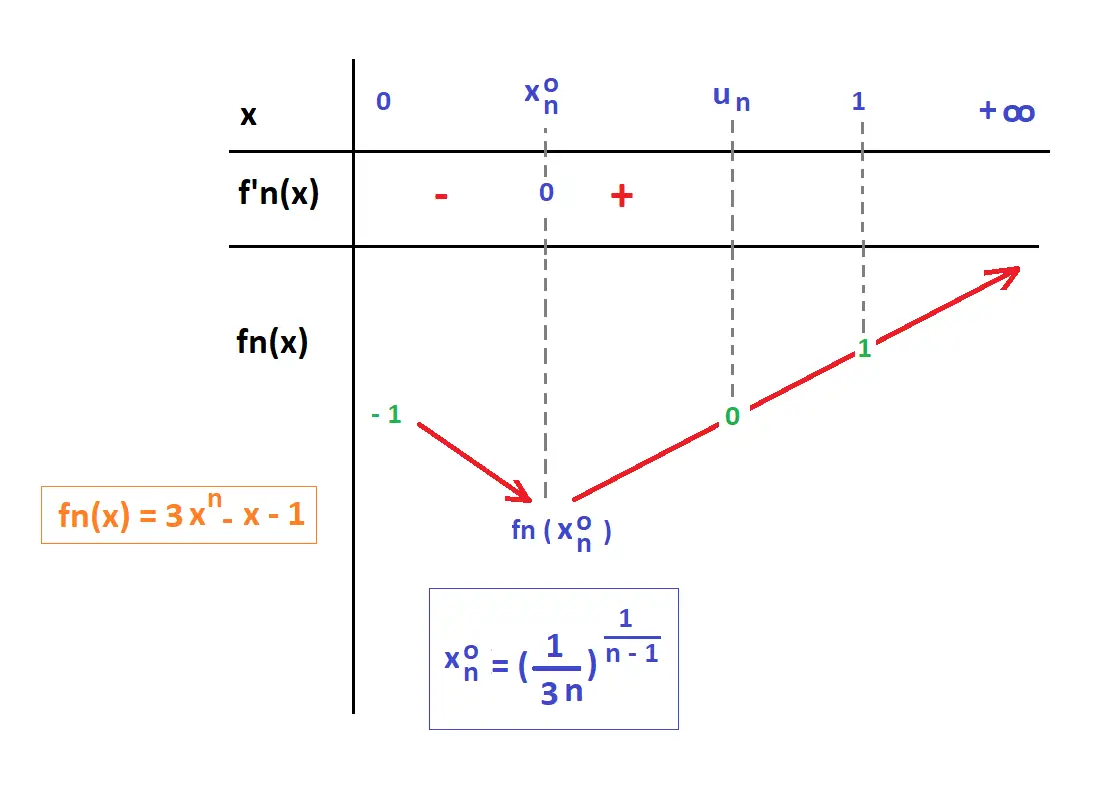
1. Tableau de variation de de fn sur R+:
1.1. Limites aux bornes:
fn(0) = - 1, ∀ n ∈ N*
lim fn(x) = 3 lim (xn) = + ∞
x → +∞
∀ n ∈ N*
1.2. Dérivée de la fonction fn(x) = 3xn - x - 1:
f'n(x) = 3nxn-1 - 1
f'n(x) = 3nxn-1 - 1
• Extremums de fn:
f'n(x) = 0 ⇒ 3n xn-1 - 1 = 0
xn-1 = 1/3n ⇒ x = (1/3n)1/(n-1), soit
∀ n ∈ N*\{1} f'n(xon) = 0 ,
avec
xon = (1/3n)1/(n-1), minimum de la fonction.
Pour n = 1 f1 (x) = 3x - x - 1 = 2x - 1 et f1'(x) = 2
fn(xon) = 3(xon)n - (xon)) - 1 =
3((1/3n)1/(n-1))n - ((1/3n)1/(n-1)) - 1 =
(1/3n)1/(n-1)(3(1/3n)n - 1) - 1.
2. Nous avons:
• (1/3n)1/(n-1) > 0
• 3(1/3n)n < 1 → ( 3(1/3n)n - 1 < 0
⇒ fn(xon)< 0
∀ n ∈ N*\{1} fn(xon)< 0 .
La fonction est strictement décroissante de 0 à xon et
strictement croissante de xon à +∞
Dans l'intervalle In = [xon, + ∞[, la fonction fn(x) est
monotone strictement croissante. C'est donc une bijection
de In vers fn(In) = [fn(xon), + ∞[. Il existe donc un unique xn ∈ tel que fn(xn) = 0. Appelons un
ce nombre xn. L'ensemble de ces un constitue une suite (Un).
Remarque: On peut appliquer ici le théorème de "Bolzano".
Ecrivons :
fn(un) = 0
3. fn(0) = - 1 , fn(1) = 1 ∀ x ∈ R+ et
fn(un) = 0
On a donc : - 1 < 0 < 1
fn est strictement croissante de xon à +∞ ⇒
fn(0) < fn(un) < fn(1)
L'application inverse permet d'ecrire:
fn-1 o fn(0) <
fn-1 o fn(un) <
fn-1 o fn(1)
D'où :
0 < un < 1
4.
4.1. On a:
fn(x) = 3 xn - x - 1
fn+1(x) = 3 xn+1 - x - 1
On retranche membre à membre:
fn+1(x) - fn(x) =
3 xn+1 - x - 1 - 3 xn + x + 1 =
3 xn+1 - 3 xn = 3 xn (x - 1 )
• 3 xn > 0
• x - 1 < 0
D'où :
3 xn+1 - 3 xn < 0
fn+1(x) - fn(x) < 0
fn+1(x) < fn(x)
4.2. Nous avons:
fn(un) = 3(un)n - un - 1 = 0
fn+1(un+1) = 3(un+1)n+1 - un+1 - 1 = 0
On a aussi :
fn+1(un) = 3(un)n+1 - un - 1 =
(un)(3 un - 1) - 1
• un > 0 et
• 3 un - 1 < 0 ⇒
fn+1(un) < 0 = fn+1(un+1)
D'où :
fn+1(un) < fn+1(un+1)
L'inverse de fn+1 fn+1-1 est aussi monotone
et strictement croissante de [fn+1(xon), + ∞[. Il vient donc:
fn+1-1 o fn+1(u) <
fn+1-1 o fn+1(un+1)
D'où :
un < un+1
un < un+1
4.3. La suite (Un) est donc une suite croissante majorée par 1, puisque
0 < un < 1. Selon le théorème de convergence monotone, elle doit donc converger vers une borne supérieure "l".
Nous allons chercher ce nombre "l". On va d'abord l'encadrer.
Nous avons: ∀ n ∈ N* un ≤ l
D'autre part, 0 < un < 1
Donc: 0 ≤ l ≤ 1
• Pour n = 1 un = u1 et
f1 (u1 ) = 3u1 1 - u1 - 1
= 2u1 - 1
→ u1 = 1/2
(Un) est strictement croissante, 1/2 est la plus petite valeur de un.
Donc 1/2 < l
On a donc 1/2 ≤ l ≤ 1
1/2 ≤ l ≤ 1
Le raisonnemnet par l'absurde pourrait fixer la valeur de l.
On suppose que l ≠ 1
Avec 1/2 ≤ l ≤ 1 , on aura:
(1/2)n ≤ unn ≤ ln ≤ 1n
• lim (1/2)n = 0
n→ +∞
• lim (1)n = 0
n→ +∞
Par le théorème du Sandwich, On a
• lim unn < 1
n→ +∞
On peut ecrire:
• lim 3 unn < 3
n→ +∞
On remplace dans l'équation fn (un) = 0
3unn - un - 1 = 0
On passe au limites:
0 - lim un - 1 = 0
n → ∞
- l - 1 = 0 ⇒ l = - 1
On a supposé que l ≠ 1 , mais on trouve l = - 1 , c'est
donc absurde. l ≠ 1 est faux et l = 1 est vraie. Ainsi,
la suite ((Un)) converge .
lim (Un) = 1
n → + ∞
-- Abdurrazzak Ajaja
Septembre 2024
|
|