Exercices
Mathématiques
Baccalauréat 2
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Math - Fonction implicite
Analyse
Suite implicite
Suite de fonctions
Exemple:
On considère une suite de fonction gn de R+ vers R, telle que :
gn(x) = 2x3 - x2 + 2(n + 1)x - 1 ,
n ∈ N*
0. Allure de la fonction fn (x) sur R+:
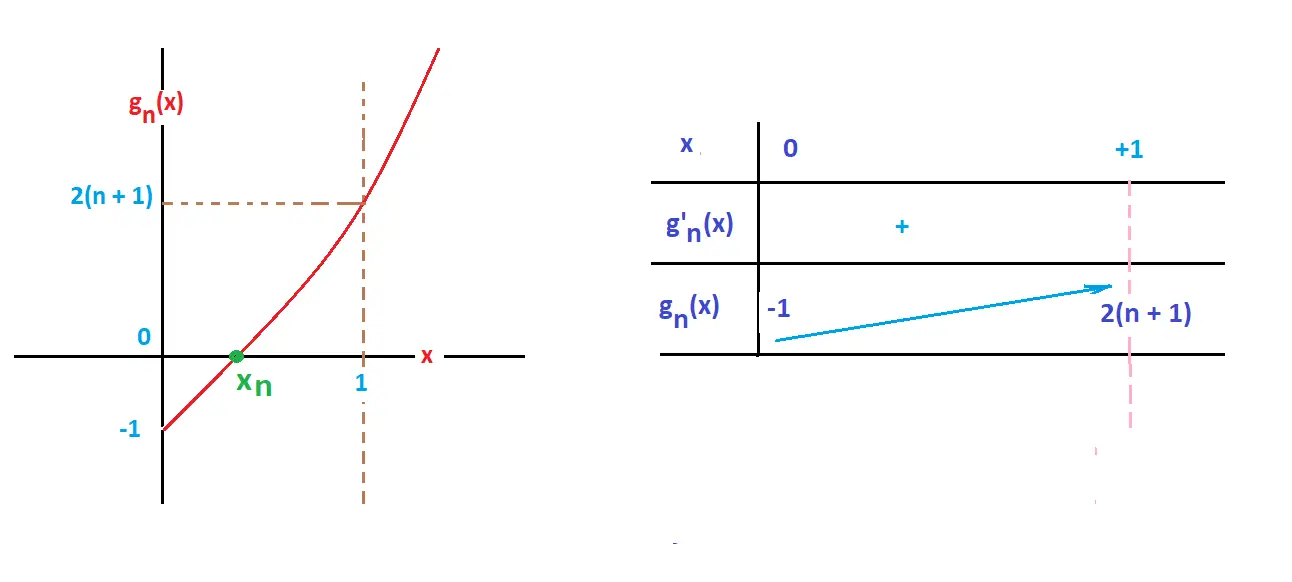
1. La foncton est polynomiale, donc dérivale en tout point de R"
g'n(x) = 6 x2 - 2x + 2(n + 1) .
Son équation quadratique est g'n(x) = 0 . Le discriminant Δ vaut:
(-2)2 - 4 (6)(2(n + 1))= 20 - 48 n < 0.
g'n(x) est du signe de "6", donc positive ent tout temps.
Ainsi gn(x) est strictement croissante.
gn(x) est strictement monotone croissante dans R et dans l'intervalle ouvert
]0,1[. C'est donc une bijection de ]0,1[ vers ]gn(0 = -1 , gn(1) = 2(n +1)[.
Il existe donc un seuil xn tel que :
gn(xn) = 0
Remarque: on peut appliquer le théorème des valeurs intermédiares pour prouver
cette affirmation.
2. Nous avons:
gn(x) = 2x3 - x2 + 2(n + 1)x - 1. Donc:
gn+1(x) = 2x3 - x2 + 2(n + 2)x - 1
On fait la différence:
gn+1(x) - gn(x) = x(2n + 4 - 2n - 2)
= 2x > 0 puisque x ∈ ]0,1[, donc > 0.
⇒ gn+1(x) - gn(x) > 0
gn+1(x) - gn(x) > 0
3. Suite (xn)
Nous avons:
gn(x) = 2x3 - x2 + 2(n + 1)x - 1
gn(xn) = 0 = 2xn3 - xn2 + 2(n + 1)xn - 1
(1)
gn(xn+1) = 2xn+13 - xn+12 + 2(n + 1)xn+1 - 1
(2)
gn+1(xn+1) = 0 = 2xn+13 - xn+12 + 2(n + 2)xn+1 - 1
(3)
On remplace dans (2):
gn(xn+1) = 2(n + 1) xn+1 - 2(n + 2)xn+1 =
- 2 xn+1 < 0 puisque xn+1 <0.
gn(xn+1) <0 = gn(xn)
gn(xn+1) < gn(xn)
La fonction gn(x) est bijective. gn-1(x) l'est aussi.
On aura donc:
gn-1 o gn(xn+1) <
gn-1 o gn(xn)
C'est à dire:
xn+1 < xn
La suite (xn) est monotone décroissante.
4. Nous avons
gn (1/(n + 1)) = 2(1/(n + 1)-3 - (1/(n + 1))2 + 2 - 1
= (1/(n + 1))2 (2/(n + 1) - 1) + 1
= (2 + 2n + 3n2 + n3)/(1 + n) > 0 , puisque n ∈ N*
> 0
gn (1/(n + 1)) > 0 = gn (xn)
gn est bijective, la fonction inverse gn-1 l'est aussi:
. Donc:
(1/(n + 1)) > xn , ou
xn < 1/(n + 1)
Sur ]0,1[ , xn est décroissante et est minorée par 0.
Lim xn = lim (1/(n + 1)) = 0
n → ∞
La suite (xn) converge vers 0.
-- Abdurrazzak Ajaja
Septembre 2024
|
|