Exercices
Mathématiques
Baccalauréat 2
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Math - Fonction implicite logarithme
Analyse
Fonction logarithmique
Fonction implicite
Exemple
On considère la fonction f définie sur R+ par
f(x) = - x ln(x)
, avec
f(0) = 0
Partie (1)
1) a) Dérivabilité de f à droite de x0 = 0
f est continue et dérivable en tout point de so Df = R+.
f'(x) = - ln(x) - x (1/x) = - ln(x) - 1
f'(x) = - ln(x) - 1
On a:
lim ln(x) = - ∞
x → 0+
lim f'(x) = - (- ∞) - 1 = +∞
x → 0+
b) Tableau de variation:
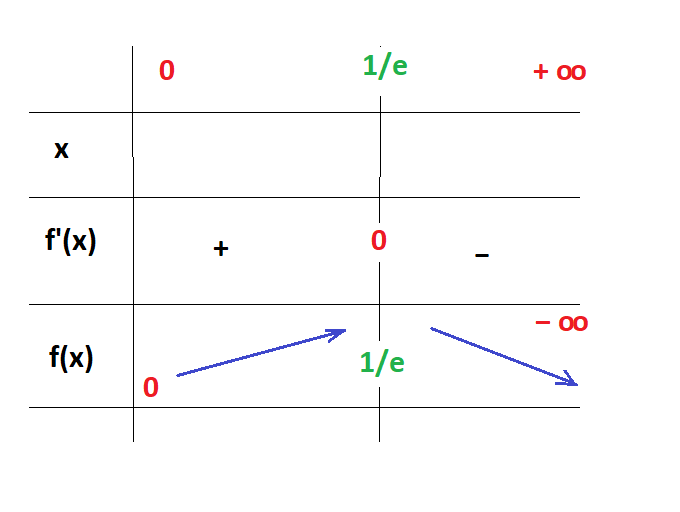
2) a) Cf étant la courbe de la fonction fet Δ la droite d'équation y = x .
La position de Cf par rapport à Δ est donnée par la différence de leurs équations respectives, soit:
d(x) = - x ln(x) - x
d(x) = - x(ln(x) + 1)
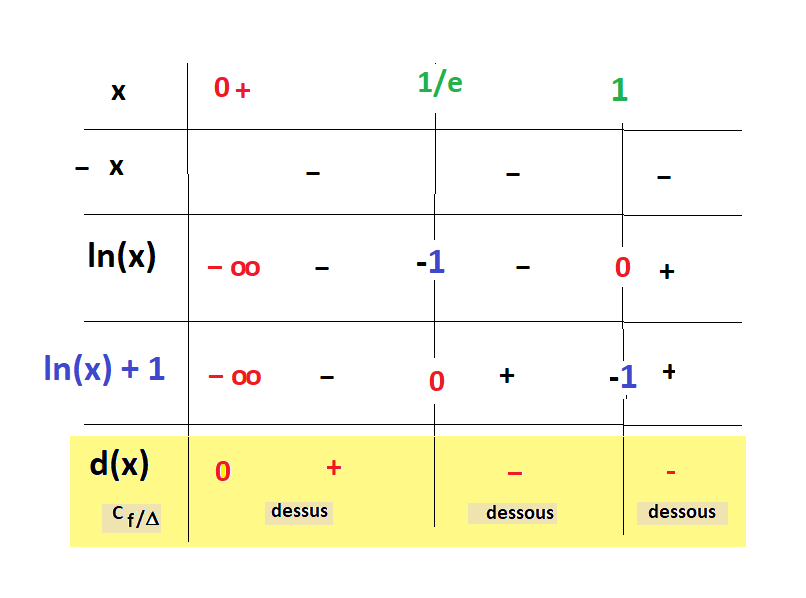
Il vient donc : Cf est en dessus de Δ
lorsque d(x) est positive, c'est à dire dans [0; 1/e], et au dessous dans [1/e; +∞[.
b) Courbe Cf :
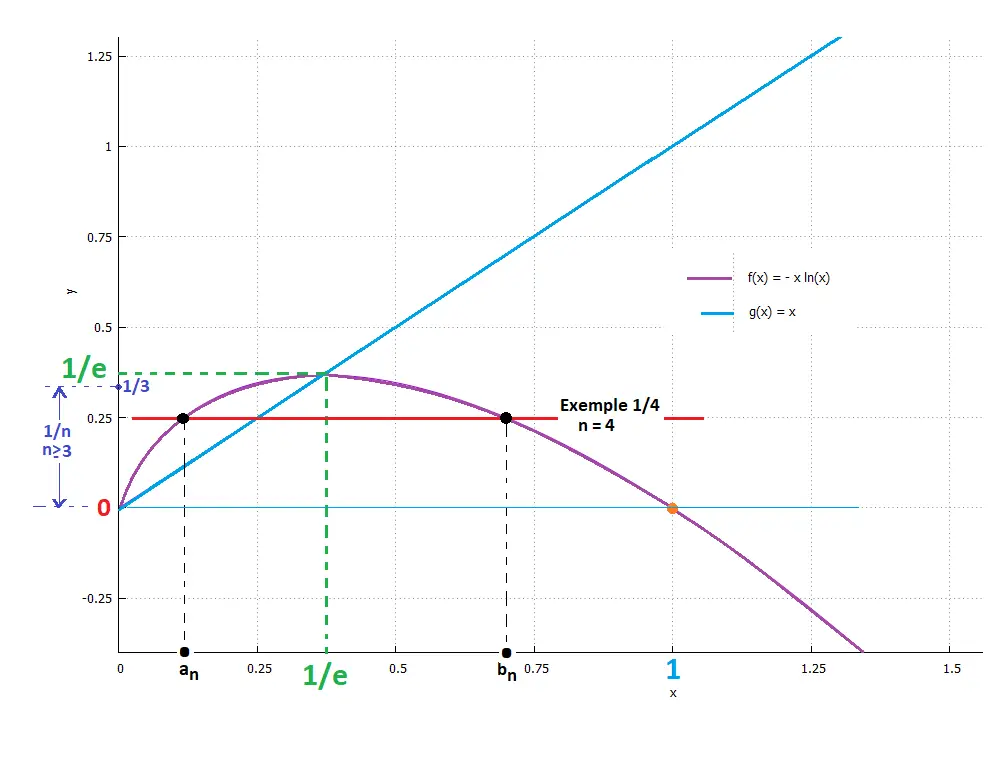
3) Soit (Un)n le suite d/finie par :
U0 = 1/e2 et Un+1 f(Un)
a) Démontrons que:
∀ n ∈ N :
0 < Un < 1/e
Par récurrence:
• Initialisation: Vraie pour n = 0 , puisque
U0 = 1/e2
1/e2 > 0 et
1/e < 1/e2
Donc:
0 < U0 < 1/e
• Hérédité :
On suppose la double inégalité est vraie pour n, et on va la démontrer aussi vraie pour n+1:
0 < Un < 1/e : vraie,
Dans l'intervalle [0; 1/e], f est strictement croissante. Donc:
0 < Un < 1/e ⇒
f(0) < f(Un) < f(1/e), ou
0 < Un+1 < f(1/e) = 1/e Vraie
• Conclusion:
∀ n ∈ N :
0 < Un < 1/e
b) Convergence de (Un)n :
Un+1 - Un = f(Un) - Un =
- Un ln(Un) - Un =
- Un(ln(Un) + 1)
On a: Un < 1/e ⇒
ln(Un) < ln(1/e) - 1 , puisque ln(x) est une fonction continue est croissante dans R+.
Donc:
(ln(Un) + 1) < 0
D'où : - Un(ln(Un) + 1) > 0
Un+1 - Un > 0 ⇒
(Un)n est une suite croissante
Si une suite est croissante et majorée par M = 1/e , alors elle converge.
c) On a:
lim (Un) = 1/e
n → +∞
Partie (2)
Soint n un entier naturel tel que : n ≥ 3
Ce qui assure que :
1/n ≤ 1/e,
pour rester dans le domaine image de f qui est
If = [1/e, +∞[
1) L'équation f(x) = 1/n admet deux solutions puisque f(x) = - x ln(x) admet un extrémum, ici un maximum, dans R+.
Soient an et bn ces deux solutions, avec an < bn
an et bn satisferont la formule suivante :
f(an) = f(bn = 1/n
- an ln(an) = - bn ln(bn) = 1/n
ln(an- an) =
ln(bn- bn) = 1/n
an- an =
bn- bn = e1/n
ou
anan =
bnbn = e- 1/n
2) f(an) = 1/n
f(an+1) = 1/(n + 1)
On a 1/(n + 1) < 1/n , donc:
f(an+1) < f(an)
Dans [0; 1/e], f est strictement croissante, bijective, sa fonction inverse permet d'ecrire:
f-1 o f(an+1) < f-1 o f(an) , soit
an+1 < an , c'est à dire que la suite (an)n est décroissante.
(an)n est décroissante.
La suite est décroissante minorée par m = 1/n alors elle est convergente.
lim (an) = 0
n → +∞
3) a) Dans R+ , ex > x2, ce qui donne:
2 ln(x) < x
ln(x2) < x
avec
x = 1/n , on aura:
ln(1/n2) < 1/n = f(an)
= - an ln(an)
= ln(1/ann)
ln(1/n2) < 1/n = ln(1/anan)
D'où:
1/n2 < 1/anan
Noua avons
an < 1 . Donc:
1/anan < an
Il vient:
1/n2 < an
1/n2 < an
b) On a 2 ln(x) < x
On remplace x par n, on obtient:
2 ln(n) > n. On prend le ln(x) qui est une fonction croissante dans R+ :
ln(2) + ln(ln(n)) < ln(n)
- ln(2) - ln(ln(n)) > - ln(n)
- ln(2) - ln(ln(n)) - ln(n) > - 2ln(n)
Ou
(- ln(2) - ln(ln(n))/ln(n) - 1 > - 2 (E1)
Nous avons:
1/n2 < an ⇒
ln(an) > - 2 ln(n)
Ou ln(an)/ln(n) > - 2
(ln(an)/ln(n) > - 2 (E2)
On peut avoir:
ln(an)/ln(n) ≥ (- ln(2) - ln(ln(n))/ln(n) - 1
On rappelle que :
• ln(x) = + ∞
x → + ∞
• ln(x)/x = 0
x → + ∞
Il vient:
lim ln(an)/ln(n) = - 1 + 0 + 0 = - 1
n → + ∞
lim ln(an)/ln(n) = - 1
n → + ∞
4) a) Selon le graphe, (bn)n est croissant et converge vers 1.
lim Un = 1
n → +∞
b) ln(x) est continuesur [bn; 1] et dérivale sur ]bn,1[ . En appliquat le TAF , le théorème des accroissements finis, ∃ c'= ln'(c') ∈ [bn; 1] tel que:
(ln(1) - ln(bn))/)1 - bn) = c' = ln'(c') , avec c' = 1/c, on peut ecrire:
- ln(bn)/(1 - bn) = c'
Ou
pour n > 2
ln(bn)/(bn - 1)/ ln(bn) = c
On a:
lim (bn - 1)/ln(bn) = 0/0,
n → +∞
C'est une forme indeterminée. On lève l'indetermination par le théorème de l'Hopital:
On change de variable: x = bn:
lim (x - 1)/ln(x) = 1/(1/x) = x
x → 1
=
lim (bn - 1)/ln(bn) = bn = 1,
n → +∞
c = 1 ⇒ bn - 1 = ln(bn)
On a f(bn) = 1/n = - bn ln(bn)
Donc: - 1/bn = n ln (bn) = n (bn - 1)
ou - 1/bn = n ln (bn) = n (bn - 1)
- 1/bn = n (bn - 1)
D'où :
- 1/bn = n ln (bn) =
lim n (bn - 1)= lim -1/bn = -1/1 = - 1
n → +∞
lim n (bn - 1) = - 1
n → +∞
-- Abdurrazzak Ajaja
Décembre 2024
|
|