Exercices
Mathématiques
Baccalauréat 2
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Math - fonction logarithmique
Analyse
fonction logarithmique
Suites
Rappels:
1) lim ln(x) = - ∞
x → 0+
2) lim ln(x) = ∞
x → ∞
3) lim ln(x)/x = - ∞
x → 0+
3) lim ln(x)/x = indéterminé
x → ∞
La règle de l'Hospital donne :
lim ln(x)/x = lim 1/x = 0
x → ∞
4) lim x ln(x) = + ∞
x → ∞
5) lim x ln(x) = indeterminé
x → 0+
Avec X = 1/x , on aura:
lim x ln(x) = lim - ln(X)/X = 0 (d'après la règle 2)
X → + ∞
lim x ln(x) = 0
x → 0+
On cherche la limite suivante:
lim (1 + 1/x)x = e;
x → +∞
On pose y = (1 + 1/x)x
Prenons le ln, en posant x = 1/X:
ln y = x ln (1 + 1/x) = ln(1 + X)/X =
(ln(X + 1) - ln(1))/(X - 0)
lim (ln(X + 1) - ln(1))/(X - 0) = ln'(X + 1) = 1
X → 0
D'où
lim ln y = 1
X → 0
ou
lim ln y = 1
x → +∞
En prenant l'exponentielle:
lim y = e
x → +∞
lim (1 + 1/x)x = e
x → +∞
lim (1 + 1/(-x))-x = e
x → - ∞
De même,
On cherche la limite suivante:
lim (1 + 1/x)x
x → + ∞
= lim (1 + 1/(-x))-x = e
- x → + ∞
lim (1 + 1/x)x = e
x → - ∞
Exemple
Partie 1
Soit f une fonction définie par
f(x) = ln(1 + x) - x/(1 + x)
1. Domaine de définition de la fonction f Df:
a) 1 + x > 0 et
b) x ≠ - 1
En tout, x > - 1 . Donc :
Df = ]- 1, +∞[
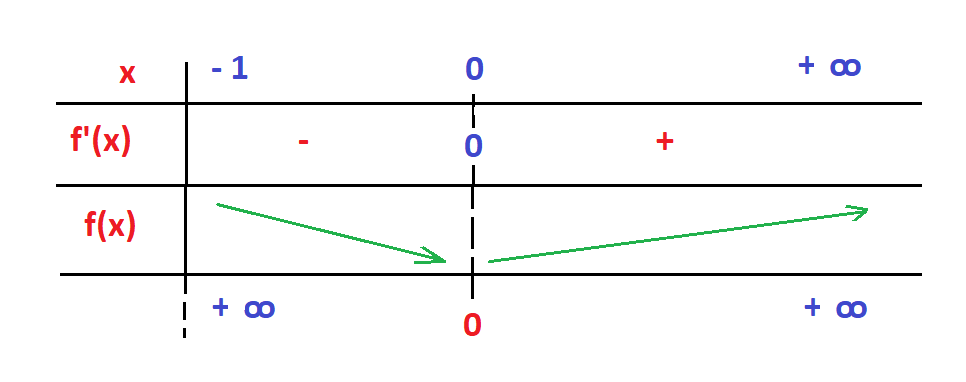
2. Variation de la fonction f:
On dérive:
f'(x) = 1/(1 + x) - ((1 + x) - x)(1 + x)2 =
1/(1 + x) - 1/(1 + x) 2 = x/(1 + x)2
f'(x) = x/(1 + x)2
(1 + x)2 > 0, donc les variations de f sont celles de x:
Dans Df = ]- 1, +∞[:
• x < 0, la fonction f est décroisante.
• x > 0, la fonction f est croisante.
• x = 0, la fonction f présente un minimum.
Limites:
On a:
f(x) = ((x + 1)ln(1 + x) - x)/(x + 1) =
1.
lim (x + 1)ln(1 + x)
x → (- 1)+
Avec X = x + 1 , on a:
= lim X ln X = 0
x → 0+ , d'après la règle 5 dans les rappels .
Donc:
lim f(x) = lim ((x + 1)ln(1 + x) - x)/(x + 1)
x → (- 1)+
= lim f(x) = (0 - (- 1)+)/0+
= + /0+ = + ∞
lim f(x) = + ∞
x → (- 1)+
2.
lim ln(x + 1) = + ∞
x → +∞
lim x/(x + 1) = lim x/x = 1
x → +∞
Donc:
lim f(x) = + ∞ - 1 = + ∞
x → +∞
lim f(x) = + ∞
x → +∞
Tableau de variation:
Partie 2
Soit g une fonction définie par
g(x) = (1 + 1/x)x
1. Domaine de définition de la fonction f Dg:
a) 1 + x > 0 et
b) x ≠ 0
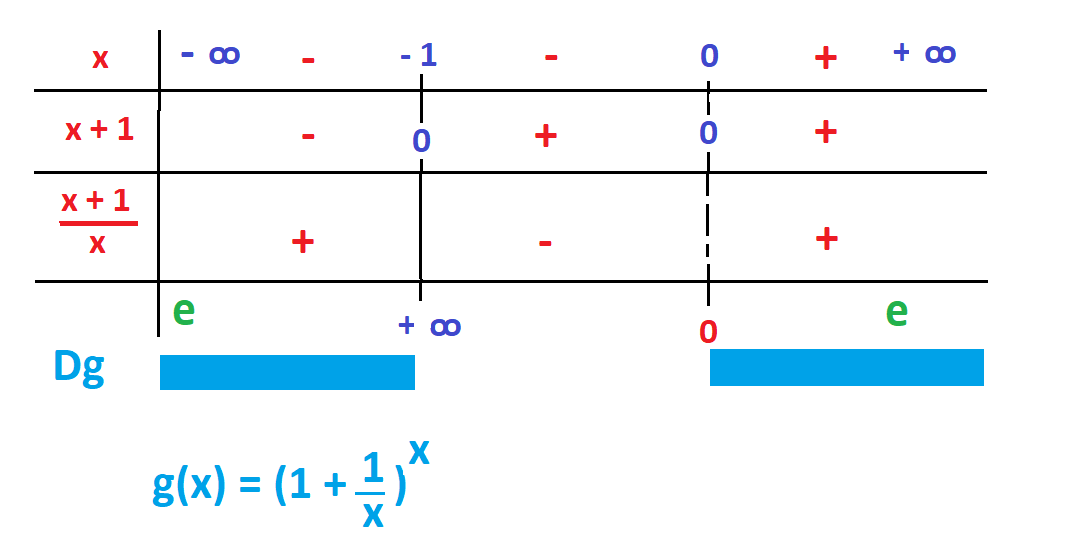
En tout, x < - 1 and x > 0. Donc :
Df = ]- ∞ -1[ ∪ ]0; +∞[
Limites:
On a:
g(x) = (1 + 1/x)x
a) lim (1 + 1/x)x =
x → -∞
lim (1 + 1/(-x))(-x) = e
x → +∞
b) lim (1 + 1/x)x = +∞
x → -1(-);
c) lim (1 + 1/x)x = 0;
x → 0+;
d) lim (1 + 1/x)x = e
x → +∞
Dérivée:
g(x) = (1 + 1/x)x
On pose:
y = g(x) = (1 + 1/x)x
ln y = ln(g(x)) = x ln (1 + 1/x)
On dérive:
(ln y)' = d(ln(y))/dx = (x ln (1 + 1/x))' =
ln (1 + 1/x) + x (-1/x2)/(1 + 1/x) =
ln (1 + 1/x) - 1/(x + 1)
(ln y)' = ln (1 + 1/x) - 1/(x + 1)
D'autre part,
(ln y)' = d(ln(y))/dx = ln(g(x))/dx = g'(x)/g(x)
D'où:
g'(x)/g(x) = ln (1 + 1/x) - 1/(x + 1) .
Donc:
g'(x) = g(x) (ln (1 + 1/x) - 1/(x + 1))
g'(x) = (1 + 1/x)x [ln (1 + 1/x) - 1/(x + 1)]
k(x) = (1 + 1/x)x est toujours positive, reste à étudier le signe de
d(x) = ln (1 + 1/x) - 1/(x + 1).
On a :
• ln (1 + 1/x) = - ln (x/(x + 1))
• 1/(x + 1) = 1 - x/(x+1)
Donc :
d(x) = ln (1 + 1/x) - 1/(x + 1) =
- ln (x/(x + 1)) - (1 - x/(x+1)) =
- ln (x/(x + 1)) - 1 + x/(x+1)
d(x) = - ln(x/(x + 1)) - 1 + x/(x+1)
avec le changement de variable: t = x/(x + 1), on aura:
d(t) = (t - 1) - ln(t)
La courbe de y1 = t - 1 est toujours au dessus de celle de
y2 = ln(t), doc d(t) est positive. Par conséquent,
d(x) = - ln(x/(x + 1)) - 1 + x/(x+1) ≥ 0
Donc g'(x) = k(x) . d(x) ≥ 0 ⇒ g est croissante.
La fonction g(x) est croissante.
2) Montrons par récurrence que
2 ≤ (1 + 1/n)n ≤ e
, avec n ∈ N*
• n = 1 : 2 ≤ 2 ≤ e , vraie
• 2 ≤ (1 + 1/n)n ≤ e supposée vraie
• 2 ≤ (1 + 1/(n+1))n+1 ≤ e ?
La fonction g est bornée entre 2 et e. Elle est croissante:
g(n) ≤ g(n + 1)
On peut donc ecrire:
2 ≤ g(n) ≤ e ou
2 ≤ g(n)≤ g(n+1) ≤ e ou
2 ≤ (1 + 1/n)n ≤ (1 + 1/(n+1))n+1 ≤ e
Elle est donc vraie pour n + 1.
∀ n ∈ N* 2 ≤ (1 + 1/n)n ≤ e
3)
On va faire le produit Π de 1 à n des trois membres de l'inégalité précédente:
D'abord:Π((n + 1)/n)n de 1 à n
Π((n + 1)/n)n de 1 à n =
(2/1)1 x (3/2)2 x
(4/3)3 x (5/4)4 x ... x (n + 1)n/nn =
1/2 x 1/3 x 1/4 x ... x (n + 1)n/n = (n + 1)n/n!
Π ((n + 1)/n)n = (n + 1)n/n!,
de 1 à n
La formule précédente :
∀ n ∈ N* 2 ≤ (1 + 1/n)n ≤ e
devient :
Π 2 ≤ Π (1 + 1/n)n ≤ Π e
de 1 à n
2n ≤ Π ((n + 1)n/n) ≤ en
de 1 à n
2n ≤ (n + 1)n/n! ≤ en
ou
1/en ≤ n!/(n + 1)n ≤ 1/2n
ou encore:
(n + 1)n/en ≤ n! ≤ (n + 1)n/2n
Finalement:
((n + 1)/e)n ≤ n! ≤ ((n + 1)/2)n
4) On pose :
an = ((n + 1)/e)n
bn = ((n + 1)/e)2
avec: an < bn
On a:
((n + 1)/e)n ≤ n! ≤ ((n + 1)/2)n
ou:
an/n! ≤ 1 ≤ bn/n!
On a:
lim an/n! = lim an/n! = 0
lim an/n! = 0
Partie 3
Soit h une fonction définie par
hn(x) = - e-x(1 + x + x2/2! + ... + xn/n!)
hn(x) peut aussi s'ecrire:
hn(x) = - e-x Σxk/k! de 0 à n
hn(x) = - e-x Σ xk/k! de 0 à n
1) On dérive:
h'n(x) = - (-)e-x(1 + x + x2/2! + ... + xn/n!)
- e-x(1 + 2x/2! + 3x2/3! + ... +nxn-1/n!)
= e-x[1 + x + x2/2! + ... + xn/n!
-(1 + 2x/2! + 3x2/3! + ... + nxn-1/n!)]
= e-x[1 + x + x2/2! + ... + xn/n!
- 1 - 2x/2! - 3x2/3! - ... - nxn-1/n!]
= e-x[ x + x2/2! + x3/3!... + xn/n!
- 2x/2! - 3x2/3! - ... - nxn-1/n!]
h'n(x) =
e-x[ x + x2/2! + x3/3!... + xn/n!
- 2x/2! - 3x2/3! - ... - nxn-1/n!]
h'n(x) peut aussi s'ecrire:
h'n(x) = e-x Σ xn/n! -
e-xΣ n xn-1/n!
=
e-x [Σ xn/n! -
Σ n xn-1/n!]
On a:
Σ n xn-1/n! = Σ xn-1/(n-1)!
Donc:
h'n(x) =
e-x [Σ xn/n! - Σ xn-1/(n-1)!]
On a aussi:
Σ xn/n! = xn/n! + Σ xn-1/(n-1)!
Il vient donc:
h'n(x)=
e-x [xn/n! + Σ xn-1/(n-1)! -
Σ xn-1/(n-1)!] =
e-x [xn/n!]
Finalement,
h'n(x)= e-x xn/n!
2) TAF: Rappel:
Pour toute fonction réelle d'une variable réelle f : [a, b] → R (a et b réels tels que a < b), supposée continue sur l'intervalle fermé [a, b] et dérivable sur l'intervalle ouvert ]a, b[, il existe un réel c dans ]a, b[ vérifiant :
(f(b)- f(a))/(b - a)= f'(c)
3) .... 
4)|1 + a + a2/2! + ... + an/!n - ea | ≤ ea an/n!
Lorsque n → + ∞, l'inégalité devient:
|1 + a + a2/2! + ... + an/!n - ea | ≤ 0 , ou
|1 + a + a2/2! + ... + an/!n| ≤ ea .
Avec :Σ ak/!k =
(1 + a + a2/2! + ... + an/!n)
On a:
lim Σ ak/!k = ea
n → +∞
lim Σ ak/!k = ea
n → +∞
Partie 4
1) Suites adjacentes:
Rappel:
Deux suites sont adjacente si l'une croit et l'autre décroit, et la limite de leur différence à l'infini est nulle .
Soit Un = Σ 1/k! de 0 à n , et
Vn = Un + 1/nn!
a) Un+1 - Un = Σ 1/k!( de 0 à n + 1) - Σ 1/k! de 0 à n ) = 1/(n + 1)!
Un+1 - Un = 1/(n + 1)! > 0 ⇒ Un est croissante
b) Vn = Un + 1/nn!
Vn+1 - Vn = Un+1 - Un + 1/(n+1)(n+1)! - 1/nn!
= 1/(n + 1)! + 1/(n+1)(n+1)! - 1/nn! =
((n+1)nn! + nn! - (n+1)(n+1)!) =
(n(n+1) + n - (n+1)(n+1) )/n(n+1)(n+1)!
=
(n2 + n + n - n2 - 2n - 1 )/n(n+1)(n+1)!
= - 1 /n(n+1)(n+1)! < 0
Vn+1 - Vn = < 0 ⇒ Un est decroissante.
c) Un - Vn = 1/nn!
Lim Un - Vn = lim 1/nn! = 0
n → +∞
Donc
Lim Un = lim Vn = 0
n → +∞
Les suites Un et Vnn sont adjacentes.
2)
On sait que :
lim Σ ak/!k = ea
n → +∞
Pour a = 1, on obtient:
lim Σ 1/k! = e1 = e
n → +∞
lim Σ 1/k! = e
n → +∞
2)Uq = Σ 1/k! de 0 à q , et
Vq = Uq + 1/qq!
qq! > 0 ⇒ Vq > Uq
À + ∞, Uq = e
Donc Vq > e
ou
∀ q ∈ N* Uq < e < Vq
3) Uq = Σ 1/k! de k 0 à q = 1/0! + 1/1! + 1/2! + 1/3! + ... + 1/q! = 1 + 1 + 1/2 + 1/6 +
... + 1/q!
Le nombre q est entier et 1/q! et donc Uq a un développement décimal infini et non périodique. De même pour Vq, puisque 1/qq! l'est aussi.
Le nombre e est irrationnel.
-- Abdurrazzak Ajaja
Decembre 2024
|
|