Exercices
Mathématiques
Baccalauréat 2
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Math - Limite d'une fonction
Limite d'une fonction
Fonctions trigonométriques et radicaux
Exemples
Rappels:


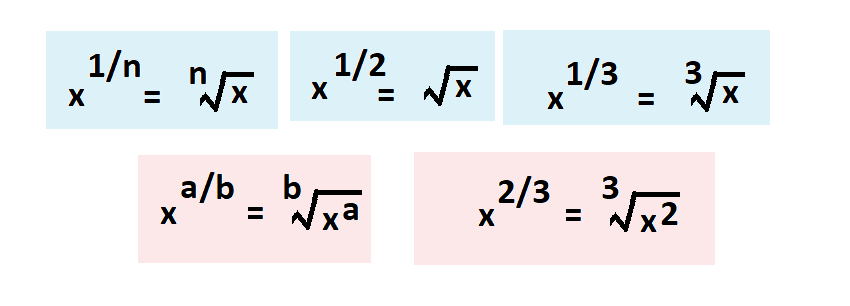
On rappelle aussi que:
•
lim (sin x)/x = 1
x → 0
•
lim (1 - cos x)/x2 = 1/2
x → 0
Dérivée de tan(x) = tan'(x) = dtan(x)/dx = 1 + tan2 x
•
tan'(x) = 1 + tan2(x)
Dérivée de tan (ax) = tan'(ax) = dtan(ax)/dx =
a dtan(ax)/d(ax) = a(1 + tan2 (ax))
•
tan'(ax) = a(1 + tan2(ax))
Exemple 1
E(x) = f(x) / g(x)
f(x) = (1 + tan x)1/3 - (1 + sin x)1/3
et
g(x) = x3
lim E(x) = 1 - 1 /0 = 0/0
x → 0
Forme indéterminée. On va lever l'indétermination:
On applique les formules:
f(x) = ((1 + tan x) - ( 1 + sin x)) /((1 + tan x)2/3 (1 + tan x)1/3(1 + sin x)1/3
+ (1 + sin x)2/3)
= (tan x - sin x ) /((1 + tan x)2/3 + (1 + tan x)1/3(1 + sin x)1/3
+ (1 + sin x)2/3)
= sin x(1 - cos x) /cos x ((1 + tan x)2/3 (1 + tan x)1/3(1 + sin x)1/3
+ ( 1 + sin x)2/3)
E(x) = (sin x/x) (1 - cos x)/x2 .
1/cos x ((1 + tan x)2/3 (1 + tan x)1/3(1 + sin x)1/3 + ( 1 + sin x)2/3)
lim E(x) = 1 x 1/2 x 1/(1 + 1 + 1) = 1/6
x → 0
lim E(x) = 1/6
x → 0
Exemple 2
E(x) = f(x) / g(x)
f(x) = (2x + 2)1/2 - (x + 7)1/3
et
g(x) = 1 - tan (πx/4)
lim E(x) = 2 - 2 /(1 - 1) = 0/0
x → 1
Forme indéterminée. On va lever l'indétermination:
Dans le souci de faire apparaitre les identités remarquables avec les radicaux, on ajoute et on retranche le nombre 2 puisque lorsque x tends vers 1, on aura:
(2x1 + 2)1/2 = 2 et
(1 + 7)1/3 = 2
Il vient:
f(x) = ((2x + 2)1/2 - 2) - ((x + 7)1/3 - 2)
= ((2x + 2) - 4)/((2x + 2)1/2 + 2)
- ((x + 7) - 8)/ ((x + 7)2/3 + (8(x + 7))1/3 + 82/3 )
= 2(x - 1)/ ((2x + 2)1/2 + 2)
- (x - 1)/((x + 7)2/3 + 2(x + 7)1/3 + 4 )
= (x - 1){2/((2x + 2)1/2 + 2)
- 1/((x + 7)2/3 + 2(x + 7)1/3 + 4)}
E(x) =
= (x - 1)/ (1 - tan (πx/4)) . {2/((2x + 2)1/2 + 2) - 1/((x + 7)2/3 + 2(x + 7)1/3 + 4)}
= {- 1 / (tan (πx/4) - 1)/(x - 1) } . {2/((2x + 2)1/2 + 2) - 1/((x + 7)2/3 + 2(x + 7)1/3 + 4)}
lim E(x) =
x → 1
{- 1/ ((π/4)(1 + tan1/2 (π/4) )) } . {2/((2 + 2)1/2 + 2) - 1/((1 + 7)2/3 + 2(1 + 7)1/3 + 4)}
= {- 1/(π/4)(1 + 1)}{1/2 - 1/(4 + 2x2 + 4 )} = {- 1/ π/2) }{1/2 - 1/12}
= {- 1/ π/2) }{5/12} = - 5π/6
lim E(x) = = - 5π/6
x → 1
-- Abdurrazzak Ajaja
septembre 2024
|
|