Articles
Sciences and sociétés
Math - fonction réciproque

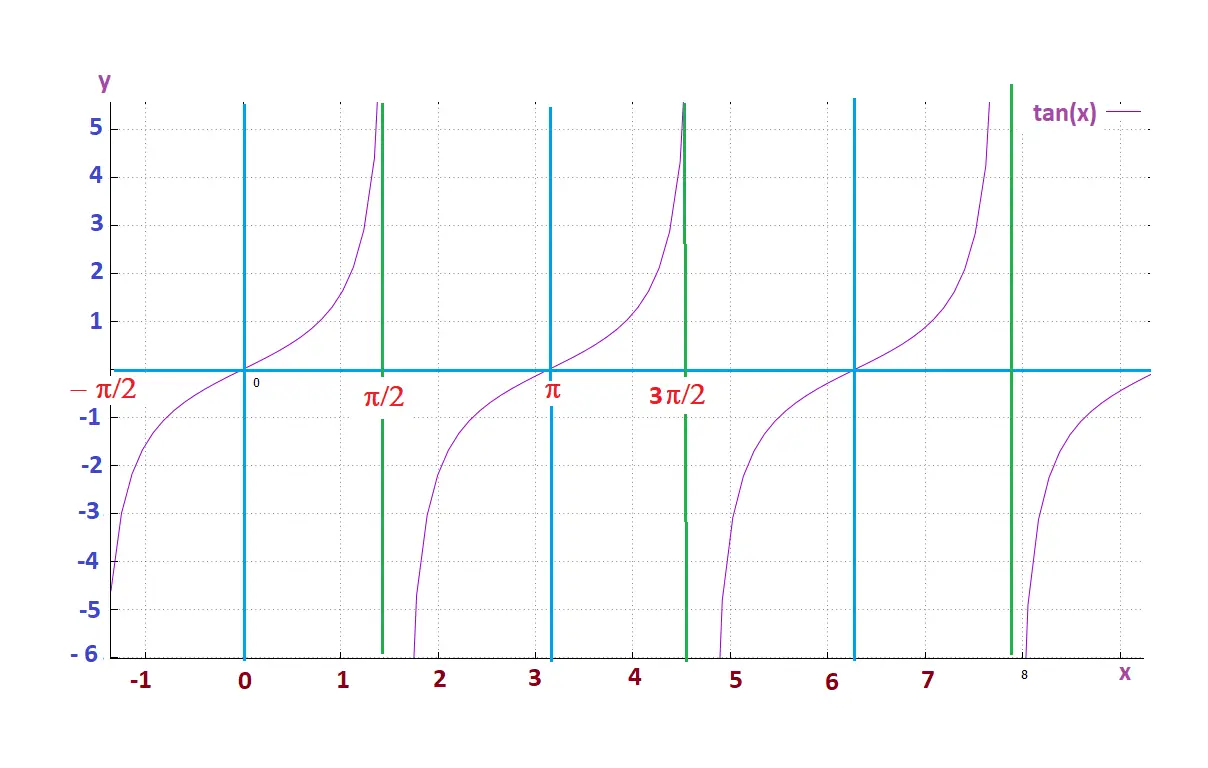
• La fonction tan(x) est périodique et de période T = π. C'est une fonction
de R \ {(2k + 1)π/2, k ∈ Z } vers R.

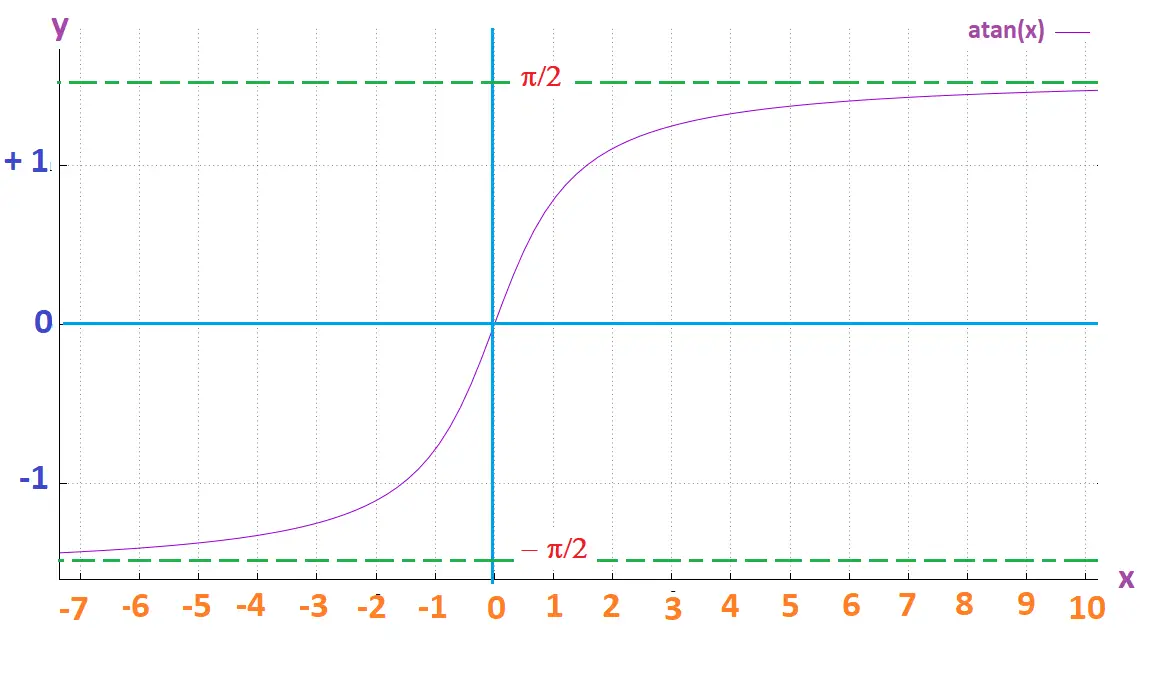
• Sa fonction inverse est Arctan (x) de R vers ]- π/2, + π/2[. On note que:

• - π/2 < Arctan (x) < + π/2

• tan (x) = sin(x)/cos(x) ≠ 0 if cos(x) ≠ 0. C'est à dire
x ≠ π/2 + 2kπ ou x ≠ - π/2 + 2kπ , avec k ∈ Z.

• Théorème de la bijection: Si f est une fonction continue et strictement uniforme sur [a, b] , alors elle estest bijection entre [a, b] et [f(a), f(b)].

• f est une bijection de E vers F ssi;

∀ y ∈ F, y = f(x) possède une unique solution. ou
∀ y ∈ F, ∃! x ∈ E / f(x) = y.

• sin² x = (1 - cos 2x)/2, ou
1 - 2 sin² x = cos 2x

• cos² x = (1 + cos 2x)/2

• tan(a + b) =
(tan a + tan b)/(1 - tan a . tan b)

• Théorème des valeurs intérmédiares

• Continuité

• Monotonie des fonctions


Exemple 1

1. On veut montrer que :

(∀ t ∈ [0, +∞[) ; (∃! α ∈ [0, π/2[ ) tel que tan(α) = √(t).

On fixe t, donc √(t) dans [0, +∞[ et on démontre qu'il existe un seul t ou √(t) sur [0, +π/2[ qui satisfait l'équation tan(α) = √(t).

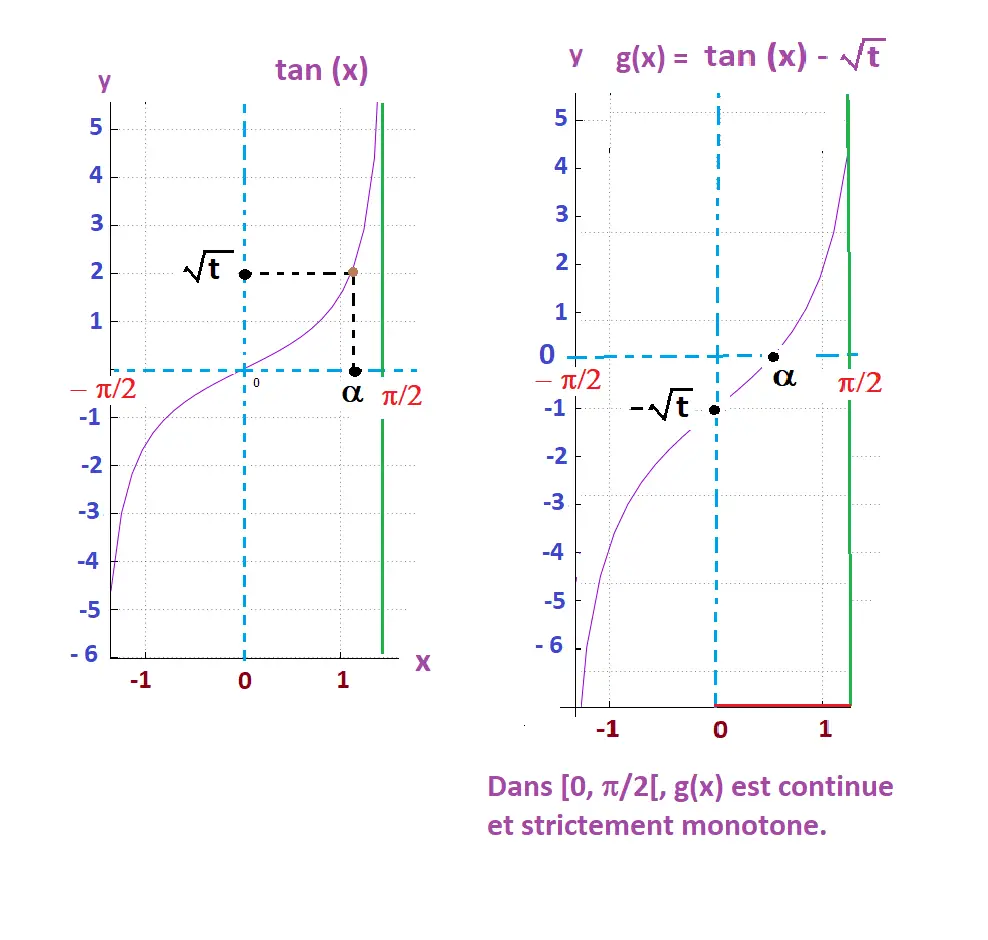
On construit la fonction g(α) = tan(α) - √(t),
de [0, π/2[ à [g(0), g(π/2)[= [- √(t), +∞[

Dans [0, π/2[ ⊂ ]- π/2, π/2[ tan(α) est continue et est strictement monotone.



t > 0 , √ (t) > 0 , then - √ (t) < 0
⇒ 0 ∈ [- √(t), +∞[

⇒ (∃! α ∈ [0, π/2[ ) tel que g(α) = tan(α) - √(t) = 0.

ou

(∀ t ∈ [0, +∞[) ; (∃! α ∈ [0, π/2[ ) tel que tan(α) = √(t).

2. On veut montrer que si tan (α) = √(t), alors

tan (α/2 + π/4) = √(t + 1) + √(t)

t ∈ [0, + ∞[

On a α = Arctan(√(t))

tan (α/2 + π/4) =
(tan (α/2) + tan(π/4) )/(1 - tan (α/2) . tan (π/4) =

(tan (α/2) + 1 )/(1 - tan (α/2)) =

(cos(α/2) + sin(α/2))/(cos(α/2) - sin(α/2))
= (1 + 2sin(α/2).(cos(α/2))/(cos²(α/2) - sin²(α/2))

= (1 + sin(α))/(1 - 2sin²(α/2))

= (1 + sin(α))/(cos(α))

= 1/cos(α) + tan(α)

On a : α = Arctan(√(t)) ⇒ cos(α) = cos(Arctan(√(t)))

Donc: 1/cos²(α) = 1 + tan²(α)

Si t ∈ [0, +∞[ alors √(t) ∈ [0, +∞[

⇒ α = Arctan(√(t)) ∈ ]0, +π/2[

α > 0 ⇒ |cos(α)| = cos (α). Alors:

1/|cos(α)| = √(1 + tan²(α). Soit:

1/cos(α) = √(1 + tan²(α))

Donc: tan (α/2 + π/4) = √(1 + tan²(α)) + tan(α)

= √(t + 1) + √(t)

tan (α/2 + π/4) = = √(t + 1) + √(t)

3. On veut montrer que :

∀ t ∈ R⁺, Arctan (√(t + 1) + √(t)) = π/4 +(1/2) Arctan(√(t)

Avec l'équation : tan (x) = tan(a) ⇒ x = a + kπ , k ∈ Z

On peut ecrire:

tan (α/2 + π/4) = tan( Arctan(√(t + 1) + √(t)))

Arctan(√(t + 1) + √(t)) = α/2 + π/4 + kπ , k ∈ Z.

Nous avons:

0 ≤ α = Arctan(√(t)) < π/2 ⇒
0 ≤ α/2 < π/4 ⇒ π/4 ≤ α/2 + π/4 < π/2

Donc k = 0.

Arctan(√(t + 1) + √(t)) = α/2 + π/4 , de R⁺ dans [π/4, π/2[

= π/4 + α/2 = π/4 + (1/2) Arctan(√(t))

∀ t ∈ R⁺, Arctan (√(t + 1) + √(t)) = π/4 +(1/2) Arctan(√(t)

4. On veut montrer que : tan(5π/12) = 2 + √3

Dans la relation juste en dessus, on fait t = 3. Il vient:

Arctan (√(4) + √(3)) = π/4 +(1/2) Arctan(√(3)

⇒ Arctan (2 + √(3)) = π/4 +(1/2) Arctan(√(3)

On utilise : tan(π/3) = √3 ou π/3 = Arctan(√3), il vient:

Arctan (2 + √(3)) = π/4 + (1/2) . π/3 = π/4 + π/6 = 5π/12

D'où:

tan(Arctan (2 + √(3))) = tan(5π/12), ou :

2 + √(3) = tan(5π/12)

tan(5π/12) = 2 + √(3)

-- Abdurrazzak Ajaja
Août 2024