Exercices
Mathématiques
Baccalauréat 2
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Math - Limites
Limites
Suite récurrente
de la forme un+1 = f(un)
Rappels:
1. Théorème de la convergence monotone
Une suite croissante et majorée est convergente.
Une suite décroissante et minorée est convergente
2. Théorème de la limite d'une fonction implicite:
Si f est continue sur un intervalle I telle que f(I) ⊂ I.
Soit (Unn≥0) une suite réelle définie par un0 ∈ I et un+1 = f(n) pour n ≥ n0
Si (Unn≥0) est convergente vers l et l ∈ I, alors l est solution dans I de l'équation f(x) = x.
Exemple 1
Soit une la fonction f définie , sur l'intervalle I = [0;1], par
f(x) = x/(1 + x + x2)
(U≥0) une suite définie par u0 = 1 et
un+1 = f(un)
1. Monotonie de la fonction f:
On dérive:
f'(x) = (1 - x2)/(1 + x + x2)
(1 + x + x2) est > 0
f'(x) = = 0 ⇒ (1 - x2)= 0
⇒ x = -1 (à rejeter) , x = 1
Tableau de variation
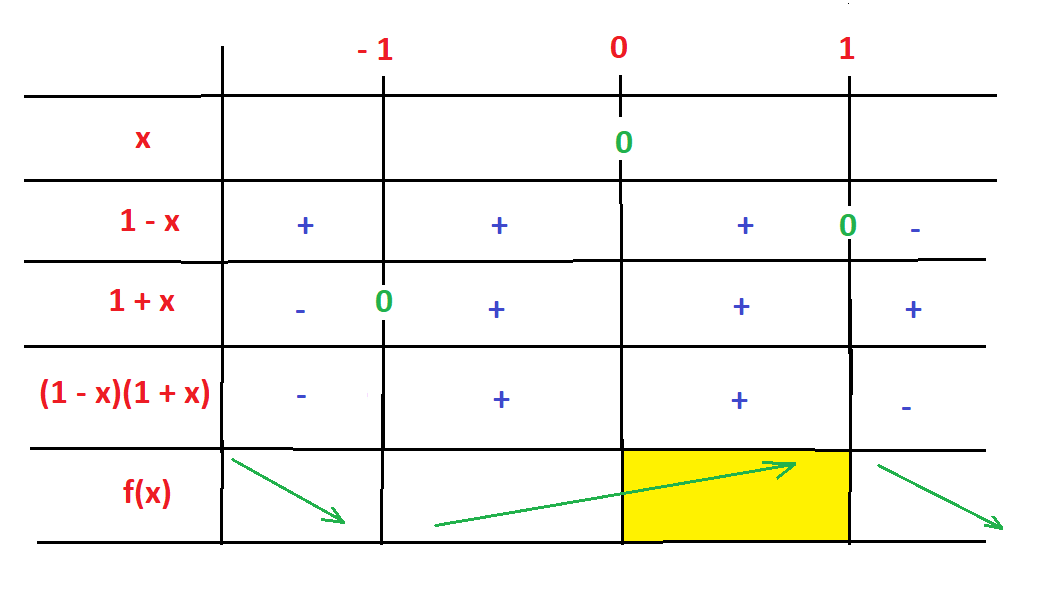
Dans l'intervalle [0;1], la fonction f est continue et strictement croissante.
f(I) = f([0;1]) = [f(0);f(1)] = [0;1/3]
⇒ f(I) ⊂ I
⇒ f(I) ⊂ I
2. a)
On veut démontrer par récurrence : 0 ≤ un ≤ 1
• Pour n = 0 ⇒ 0 ≤ u0 = 1 ≤ 1 est vraie.
• On suppose que l'inégalité 0 ≤ un ≤ 1 es vraie
• L'est-elle avec n+1 ?
f(x) ⊂ I → ∀ x ∈ I f(x) ∈ I
un ∈ I puisque 0 ≤ un ≤ 1
un ⊂ I ⇒ f(un) ∈ I
f(un) = un+1. Don
f(un) ∈ I ou ≤ un+1 ≤ 1
Conclusion : La proposition 0 ≤ un ≤ 1 est vraie pour tout
n ∈ N.
∀ n ∈ N, 0 ≤ un ≤ 1
b) On a un+1 - un = f(un) - un =
f( un) = un/(1 + un + un2) - un
= - un2(1 + un))/(1 + un + un2)
un) ≥ 0 . Donc:
f(un) ≤ 0 ⇒
La suite (un) est monotone décroissante
(un) est décroissante et minorée par 0.
D'après le théorème 1: (un) est convergente.
lim un = l
→ +∞
On cherche l.
On a: 0 ≤ un ≤ 1 . f étant strictement
croissante:
lim 0 ≤ lim un ≤ lim 1
n → +∞
devient
0 ≤ l ≤ 1
On applique le théorème 2:
f(l) = l
f(l) = l/(1 + l + l2)
On a donc + l/(1 + l + l2) = l
⇒
l2(1 + l) = 0 ⇒ l = 0
Il vient:
La suite un converge vers 0.
3. a) Nous avons f(1/k) = (1/k)/(1 + 1/k + 1/k2)= f(k) =
1/(1 + k + 1/k)
k ∈ N*, 1/k ≤ 1. Donc :
1/(1 + k + 1/k) ≤ 1/(1 + k). Il vient:
f(1/k) ≤ 1/(1 + k)
∀ k ∈ N* k ≤ 1/(1 + k)
• k = 1
f(1/k) = f(1) = 1/3 = 0.33
u1 = f(u0) = f(1) = 1/3 = 0.33
• k = 2
f(1/2) = f(2) = 2/7 = 0.28
u2 = f(u1) = f(1/3) = f(3) = 3/13 = 0.23
• k = 3
f(1/3) = = f(3) = 3/13 = 0.23
u3 = f(u2 ) = f(3/13) = f(13/3) =
(13/3) x (1/( 1 + 13/3 + (13/3)2))= 0.18
....
On aura toujours :
∀ k ∈ N* uk ≤ f(1/k)
On a: uk = f(uk-1)
La fonction f est continue et strictement croissante, sa
fonction inverse l'est aussi, d'après le théorème de la bijection :
uk ≤ f(1/k) ⇒ f(uk-1)≤ f(1/k)
f-1 o f(uk-1) ≤ f-1 o f(1/k)
D'où:
uk-1 ≤ 1/k
On aura aussi
uk ≤ 1/(1 + k)
b)Nous avons
uk+1 = f(uk)= uk/(1 + uk + uk2)
Donc:
1/uk+1 = 1/f(uk)=
(1 + uk + uk2)/uk
1/uk+1 - 1/ uk = 1 + uk ≥ 1
Avec uk ≤ 1/(1 + k), on aura :
1 ≤ 1/uk+1 - 1/uk = 1 + uk ≤
1 + 1/(1 + k)
1 ≤ 1/uk+1 - 1/uk ≤
1 + 1/(1 + k)
On fait la somme de k = 1 à k = n:
Σ 1 ≤ Σ1/uk+1 - Σ1/uk ≤
Σ1 + Σ1/(1 + k)
n ≤ Σ1/un - 1/u0 ≤
n + Σ1/(1 + k)
n ≤ Σ1/un - 1 ≤
n + Σ1/k , de k = 1 à k = n
n ≤ Σ1/un - 1 ≤
n + Σ1/k ,
de k = 1 à k = n
c) Nous avons:
un ≤ 1 , donc :
1/un ≥ 1
Pour la série , harmonique tronquée, Σ (1/k) de k = 2 à k = n
On vérifie que:
Σ (1/k) ≤ (n - 1)/2
•
n = 2 → Σ (1/k) de k = 2 à k = 2 = 1/2 ≤ (2 - 1)/2 = 1/2, vraie.
•
n = 3 → Σ (1/k) de k = 2 à k = 3 = 1/2 + 1/3 = 5/6 ≤ (3 - 1)/2 = 1 , vraie.
•
n = 4 → Σ (1/k) de k = 2 à k = 4 = 1/2 + 1/3 + 1/4 = 13/12 = 1.08 ≤ (4 - 1)/2 = 1.5 , vraie.
La double inégalité:
n ≤ Σ (1/un) - 1 ≤
n + Σ1/k ,
de k = 1 à k = n
devient
1/un - 1 ≤
n + + Σ1/k ,
de k = 1 à k = n
ou
1/un - 1 ≤
n + 1 + Σ1/k , de k = 2 à k = n
⇒
1/un - 1 ≤
n + 1 + (n - 1)/2 = (3n + 1)/2
⇒
1/un ≤
(3n + 1)/2 + 1 = (3n + 3)/2
D'où:
un ≥
2/(3n + 3)
ou
2/3(n + 1) ≤ un
2n2/3(n + 1) ≤ n2un
On passe à la limite:
lim 2n2/3(n + 1) ≤ lim n2un
n → + ∞
lim 2n2/3(n + 1) = lim 2n2/3n = lim 2n/3 = +∞
n → + ∞
+∞ ≤ lim n2un
n → + ∞
Il vient:
lim n2un = + ∞
n → + ∞
Annexe:
Théorème de la bijection
On considère une fonction f : I → R
définie sur un intervalle I.
1) f continue sur I,
2) f strictement
croissante sur I.
⇒
a) f(I) est un intervalle,
b) f : I → f(I) est bijective,
c) f-1 :f(I) → I est continue et
strictement croissante sur f(I).
ou
1) f continue sur I,
2) f strictement
décroissante sur I.
⇒
a) f(I) est un intervalle,
b) f : I → f(I) est bijective,
c) f-1 :f(I) I est continue et
strictement décroissante sur f(I).
-- Abdurrazzak Ajaja
Novembre 2024
|
|