Exercices
Baccalauréat 2
Physique
Chimie
© The scientific sentence. 2010

|
Articles
Sciences and sociétés
Physique - Mécanique
Chimie :
Concentration
Suivi temporel par dosage
Préparation:
Une transformation lente et totale de la réduction des ions peroxodisulfate en ions sulfate par les ions iodure, selon la réaction:
2 I-(aq) + S2O82-(aq)) → I2(aq) + 2SO4 2-(aq) (E1 )
À une température favorable et constante , on prépare à l'instant t = 0 , dans n béchers identiques des mélanges identiques contenant chacun un volume V1 d'une solution acqueuse (S1)d'iodure de potassium de concentration molaire C1 et
un volume V2 = V1 = V, d'une solution (S2)de peroxodisulfate de potassium de concentration molaire C2 = (1/5)C1
Chaque mélange initial ainsi obtenu noté (M) est de volume total 200 mL.
On désigne par n01 et n02 les quantités de matière initiales dans (M) des ions iodure et des ions peroxodisulfate respectivement"
Pour déterminer la quantité de matière du diiode I2 formé au cours du temps, on prend à différents instants l'un des mélanges (M) que l'on dose à l'aide d'une solution acqueuse (S) de thiosulfate de sodium de concentration molaire C0. La réaction du dosage,supposée rapide et totale est la suivante:
I2(aq) + 2S2O32-(aq) → 2 I-(aq) +
S4O6 2-(aq) (E2 )
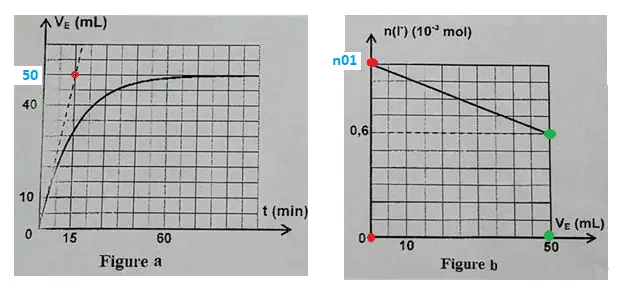
On obtient deux courbes:
a) la courbe (a) qui traduit l'évolution temporelle du volume VE (en mL) de la solution (S) de dosage versée pour atteindre l'équilibre de I2 dans (M) à un instant t quelconque
(en mn)
b) La courbe (b) qui traduit l'évolution de la quantité de matière des ions iodure n(I-) (x 10-3 mol) dans (M) en fonction de de l'évolution de VE (mL)
Exercice
1) La concentration molaire effective des ions potassium dans le mélange réactionnet à l'état initial
Iodure de Potassium (K+]0 + I-]0):
À l'état initial: [K+,I-]0 = [K+]0
= [I-] = C1
D'où
α = [K+]0/C1 = 1
2)
Les ions peroxodisulfate sont réduits. Ils consomment 2 électrons dans la
demi-réaction:
2e- + S2O82- → 2O42-
3) Le mélange est stoechiométrique.
5) Nous avons deux couples oxydant / réducteur : S2O82-/
SO4 2- et I2 / I-
6)
VEF = 50 ML D'après la courbe a)
et n(I-) = 0.6 x 10-3 moles
D'après la coube a) À l'état initial: [I-] → VE = 0
La courbe b) donne VE = 0 → n(I-) = 10-3 moles
D'une table d'avancement, on peut avoir:
7) n(I-) = n01 - 2x
x = CoVE (du dosage)
n(I-]) = n01 - 2CoVE
La table b) donne VE = 0 → n(I-]) = 10-3
d'où :
n01 = 10-3 moles
Pour n(I-) = 0.6 x 10-3 → VE = 50 mL
Donc:
0.6 x 10-3 = 10-3 - 2 C0 x 50
D'où:
Co = 4 x 10-3 mol/L
Donc :
n(I-) = 10-3 - 8 x 10-3 VE
n(I-) à t = 0 = C1 V1
10-3 mol = C1 (200 mL/2)
Donc C1 = 10-5 mol/mL = 10-2 mol/L = 10 m.mol/L
C1 = 10 m.mol/L
8)
Vitesse = (1/V) dx/dt = (1/V) Co dVE/dt =
(1/200 mL) x 4 x 10-3 mol/L dVE/dt =
2 x 10-2 mol/L2 dVE/dt =
Donc:
V = 2 x 10-2 mol/L2 dVE /dt
On prend la tangente au point o ou la tangente est maximum:
On a dVE /dt = (50 - 0)/ (15 - 0) = 50/15 = 10/3 mL/mn = 10-2/3 L/mn
Donc:
V = (2 x 10-2) x 10-2/3 = (2/3) 10-4 = 6.6 x 10-5 mol/L/mn
9) le graphe b) donne:
dn(I-)/dVE = (0.6 - 1)/(50 - 0) = - 0.4 /50 = - 8 x 10-3
Constante parce nous avons une fonction affine représentée par une droite.
10) Nous avons x(t) = Co VE (t). Nous aurons la meme courbe que VE (t) à
Co près.
-- Abdurrazzak Ajaja
Septembre 2024
|
|