Articles
Sciences and sociétés
Physique - Électricité

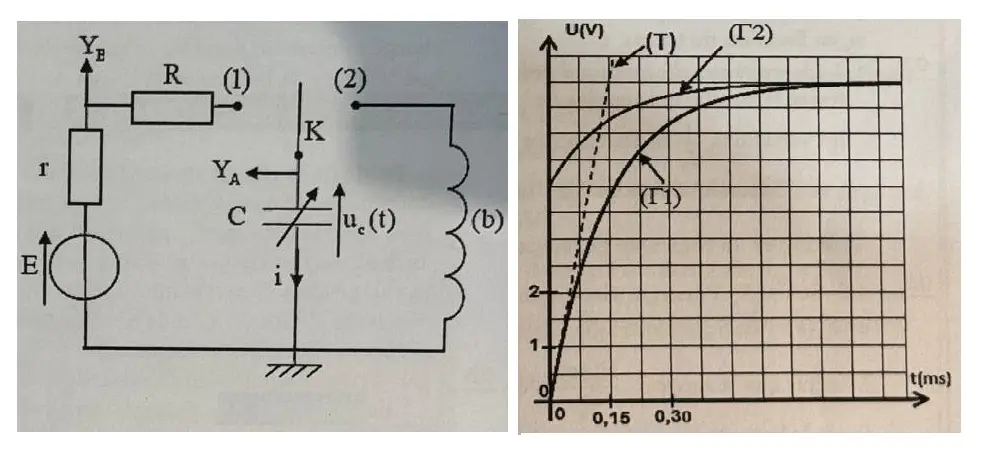
L'interrupteur est sur la position (1).

La loi d'addition des tensions s'ecrit:

Σ U_i = 0

E - ri - Ri - U_v = 0

ou

(r + R)i + U_c = E      (E1)

On sait que l'expression du courant traversant une capacité est :

i = C dU_c/dt      (E2)

On remplace dans la formule (E1) et on obtient:

(r + R)C du_c/dt + U_c = E

On arrage et on obtient l'équation différentielle relative au circuit RC:

dU_c/dt +(1/(r + R)C) U_c = E/(r + R)C      (E3)

Cette équation de charge et de décharge d'un condensateur est toujours de la forme:

U_c = E(1 - exp{- t/(r + R)C})      (E4)

On dérive :

dU_c/dt = (E/(r + R)C) exp{- t/(r + R)C}      (E5)

La formule (E2), permet d'écrire :

i = C dU_c/dt = C(E/(r + R)C) exp{- t/(r + R)C} = E/(r + R) exp{- t/(r + R)C}

i(t) = E/(r + R) exp{- t/(r + R)C}      (E6)

La courbe Γ₁ représente la variation de la tension aux bornes du condensateur C.

La courbe Γ₂ représente la variation de la tension aux bornes de la résistance r.

1. À t = 0, de la formule (E6), on obtient:

i(0) = E/(r + R) exp{- 0/(r + R)C₀} = E/(r + R)

Soit :

i₀ = E/(r + R)      (E7)

On peut trouver ce résultat avec le raisonnement suivant:

À t = 0, U_c = 0 et la formule (E1) s'ecrit:

(r + R)i₀ + 0 = E.

D'où la formule (E7) :

i₀ = E/(r + R)

2. L'équation différentielle relative au circuit RC est donnée par la formule (E3)

dU_c/dt +(1/(r + R)C₀) U_c = E/(r + R)C₀      (E3)

La lecture sur la courbe Γ₁ donne à l'infini:

U_c(∞) = 10 V

La tangente (T) à la courbe Γ₁ au point t = 0 s'ecrit à partir de la forme (E5)

dU_c/dt , en t = 0 = (E/(r + R)C₀) exp{- 0/(r + R)C} = (E/(r + R)C₀)

dU_c/dt , en t = 0 = E/(r + R)C₀

Selon le graphe de la courbe Γ₁:

Pente = dU_c/dt , en t = 0 = 3/(0.15/2) 10^-3) = 40 x 10³

D'où :

E/(r + R)C₀ = 40 x 10³

E = 10 ⇒ 10/ 40 x 10³ = (r + R)C₀

10/ 40 x 10³ = (r + R)C₀      (E8)

La courbe Γ₂ donne la tension aux bornes de la résistanne r:

U_r(t = 0) = 6 = r i₀ = rE/(r + R)

D'où :

6 = 10 r/(r + R)

Nous avons : R = 20 Ω, donc:

6 = 10 r/(r + R) ⇒ 6 = 10 r/(r + 20)

10 r = 6(r + 20) = 6r + 120 ⇒ 4r = 120

r = 30

r = 30 Ω

La formule (E8) donne :

10/ 40 x 10³ = (30 + 20)C₀

10/ 40 x 10³ x 50 = C₀

ou

C₀ = 10/ 2000 x 10³ = 5 x ^-6 F (Farad)

C₀ = 5 µF

-- Abdurrazzak Ajaja
Décembre 2024