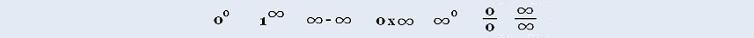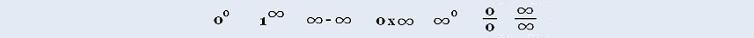Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
|
Calculus I: Asymptotes
Asymptotes are useful guides to complete the
graph of a function. An asymptote is a line to which the
curve of the function approaches at infinity or at certain points
of discontinuity.
There are three types of asymptotes: vertical asymptotes,
horizontal asymptotes and oblique asymptotes.
1. Vertical asymptote
A line x = a is a vertical asymptote of the graph
of the function f if either:
|
lim f(x) = ± ∞ or | lim f(x) = ± ∞ |
| x → a+ | x → a- |
Note:
The vertical asymbtotes exist only for the points of
discontinuity of the function.
For a rational irreducible function,
every value of x that make zero the denominator is a
verticale asymptote for this function.
A polynomial function doesn't have a verical asymptote.
A function can have one or more vertical asymptotes
Example
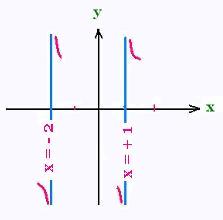
f(x) = (x + 1)/(x - 1)(x + 2)
This fonction is rational. The points x = 1 and x = - 2 are the
points of discontinuity.
At x = 1, we have:
lim f(x) = 2/0
x → 1
= 2/(3)0+ = + ∞
x → 1+
= 2/(3)0- = - ∞
x → 1-
Therefore
x = 1 is a vertical asymptote.
At x = - 2, we have:
lim f(x) = - 1/0
x → - 2
= - 1/(- 3)0+ = + ∞
x → - 2+
= - 1/(- 3)0- = - ∞
x → - 2-
Therefore
x = - 2 is a vertical asymptote.
2. Horizontal asymptote
A line y = b is a horizontal asymptote of the graph
of the function f if either:
|
lim f(x) = b | or lim f(x) = b |
| x → + ∞ | x → - ∞ |
Example
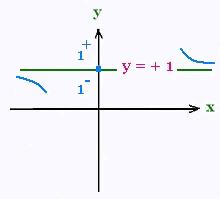
f(x) = (x + 1)/(x - 1)
We have
lim f(x) = lim (x + 1)/(x - 1) = 1
x → + ∞
And
lim f(x) = lim (x + 1)/(x - 1) = 1
x → - ∞
Therefore
y = + 1 is a horizontal asymptote.
To sketch the graph near this asymptote, we also
determine the left and right limit around the value
y = 1. Then:
lim f(x) = lim (1 + 1/x)/(1 - 1/x) = (1 + 0+)/(1 - 0+) =
1+/1- = 1+
x → + ∞
And
lim f(x) = lim (1 + 1/x)/(1 - 1/x) = (1 + 0-)/(1 - 0-) =
1-/1+ = 1-
x → - ∞
Note:
A polynomial function doesn't have a horizontal asymptote.
A rational function can have a horizontal asymptote if
the degree of the numerator is less than the degree
of the denominator.
A function can have 0, 1, or 2 horizontal asymptotes. never
more than 2.
3. Oblique asymptote
A graph of a function f has an oblique asymptote y = a x + b if
a) f(x) can take the expression: f(x) = a x + b + g(x), and
|
b) lim g(x) = 0 or | lim g(x) = 0 |
| x → + ∞ | x → - + ∞ |
Example
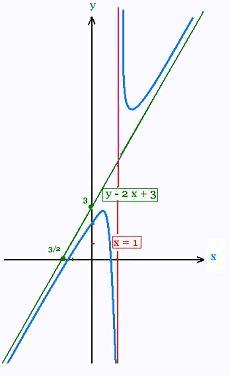
f(x) = (2 x 2 + x - 2)(x - 1)
f(x) takes the form:
f(x) = 2 x + 3 + g(x),
where
g(x) = 1/(x - 1)
We have
|
lim g(x) = 0+ → | lim f(x) = + ∞ |
| x → + ∞ | x → + ∞ |
|
lim g(x) = 0- → | lim f(x) = - ∞ |
| x → - ∞ | x → - ∞ |
|
lim g(x) = 1/0+ = + ∞ → | lim f(x) = + ∞ |
| x → 1+ | x → 1+ |
|
lim g(x) = 1/0- = - ∞ → | lim f(x) = - ∞ |
| x → 1- | x → 1- |
f(x) = 0 for x1 = (- 1 + √17)/4, and x2 = (- 1 - √17)/4
The ligne of equation y = 2 x + 3 in an oblique asymptote.
Remark:
At near infinity (±∞), the function f(x) behaves as the liear
function y = 2 x + 3, and
At near x = - 1, the fuction f(x) behaves as the function
g)x) = 1/(x - 1).
We say the dominamt term is 2 x + 3 when
x is large and g(x) at the neighborhood of x = 1.
Note:
A polynomial function doesn't have an oblique asymptote.
Any function cannot have more than two oblique asymptotes.
A rational function has an oblique asymptote if
the degree of the numerator is equal to the degree
of the denominator plus one.
A rational function cannot have a horizontal asymptote
and an oblique asymptote at the same time.
4. Exercices
|
|