Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
| Calculus: Derivative of a function
1. Definition of the derivative a function f
The derivative of a function y = f(x) denoted by
dy/dx is :
|
dy/dx = df(x)/dx =
| lim Δy/Δx
Δ x → 0
|
= lim (f(x + Δ x) - f (x))/Δ x
Δ x → 0
|
when this limit exists in R.
When the limit exists, the function is differentiable at x. If
it is differentiable for all values of its domain, we say simply that the
function is differentiable.
We use also the notations y' or f'(x) for the derivative of
the function f.
2. Derivative a function f at a point x = a
The derivative a function f at a point x = a is denoted by
f'(a) = dy/dx |x = a
|
= lim (f(x) - f(a))/(x - a)
Δ x → a
|
when this limit exists in R.
The derivative is interpreted as the instantaneous rate
of change of the function for a given value of x. From a geometric
point of view, the derivative of a function is the slope of the line
tangent to the curve of the function to a given value of x.
3. Example
What is the derivative of the function
f(x) = 2 x2 - 1
at
a) a = 1
b) a = 4 ?
f'(a) = df(x)/dx |x = a
= lim (f(x) - f(a))/(x - a)
x → a
= lim ((2 x2 - 1)- (2 a2 - 1))/(x - a)
x → a
= lim (2 x2 - 1 - 2 a2 + 1)/(x - a)
x → a
= lim 2( x2 - a2 )/(x - a)
x → a
= lim 2(x + a) = 4 a
x → a
a) At a = 1, we have:
f'(1) = 4 . 1 = 4
b) At a = 4, we have:
f'(4) = 4 . 4 = 16
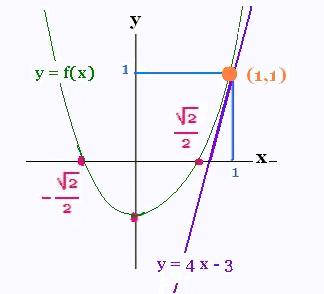
The point a = 1 has f(1) = 2 . 12 - 1 = 2 - 1 = 1
So the point (1,1) is a point on the curve.
The derivative of the function f at the point x = 1 is f'(1) = 4
which is the slope of the line tangent to the curve of f at the
point (1,1).
Therefore, we can write the equation of the
line tangent to the curve of f at the point (x,y) :
y = f'(1) x + b = 4. x + b = x + b
As the point (1,1) is on the curve, we write:
1 = 4.1 + b, so b = - 3 . The equation of the
line tangent to the curve of f at the point (1,1) is :
y = 4 x - 3
a) At the point a = 4
f(4) = 2 . 42 - 1 = 31
f'(4) = 16
so
The equation of the
line tangent to the curve of f at the point (4,31) is :
y = 16 x + b
As the point (4,31) is on the curve, we write:
31 = 16 . 4 + b
Then
b = 31 - 64 = - 33
Therefore:
y = 16 x - 33
4. Derivation and continuity of a function
If a function f is differentiable at x = a, then it is continuous
at this point.
Proof:
f is differentiable at x = a. That is
f'(a) = lim (f(x) - f(a))/(x - a) = b
x → a
We can write:
lim (f(x) - f(a))
x → a
= lim (f(x) - f(a)) . lim (x - a)/(x - a)
x → a
= lim (f(x) - f(a))/(x - a) .
x → a
|
lim (x - a)
x → a
|
= b . 0 = 0
Then:
lim (f(x) - f(a)) = 0
x → a
or
lim f(x)
x → a
|
= lim f(a)
x → a
|
That is f is continuous at the point a.
The rule is:
If a function f is differentiable at x = a, then it is contineous
at this point. But the converse is not true.
If f is discontiueous at a point then it is not differentiable at this point.
In general a function is not differentiable
at a certain point if the function:
� is discontinuous at this point,
� has a vertical tangent at this point
(where the rate of change is infinite),
� has an angular point at this point.
5. Exercices:
|
|

