Calculus: Other definitions

1. Derivatives of higher order

If f(x) is a differentiable function, its derivative is also a function and can be differentiable.

The derivative of the function f(x), when it exists, is called the
second derivative or derivative of order 2 :

f''(x) = d²f(x)/dx²

We obtain the third derivative or derivative of order 3 of f(x):

f'''(x) = f⁽³⁾(x) = d³f(x)/dx³

Similarly one can derive several times the same function to obtain the nth derivative of the function f(x), or derivative of order n:

f⁽ⁿ⁾(x) = dⁿf(x)/dxⁿ .

2. Derivative of implicit and
explicit form of a function:

2.1. Definitions

So far, all the functions studied were given in equations where the dependent variable y = f(x) was expressed in an explicit form in terms of the independent variable x. The equations were always of the form y = f (x).

Sometimes, however, the equation is not given in this form. This is the case of the equation;
xy + 2x - 5 = 0.

The equation is presented in the form f(x, y) = 0.
We say that the variable y is expressed in an implicit form of the variable x.

To move from the implicit form to the explicit form, we solve the equation for the variable y:

xy + 2x - 5 = 0.
xy = - 2x + 5
y = (- 2x + 5)/x

Now, the equation defines a function in an explicit form. This function can now be derived using the previous rules.

• A function is in an implicit form when it
is of the type f (x, y) = 0.

• A function is in an explicit form when it
is of the form y = f (x).

2.2. Implicit derivative example

To differentiate an implicit function:
a) We derive the two sides of the equation,
b) Then, we solve for a chosen variable.

3. Derivative of reciprocal functions

If the equation that we have is is provided in the form x = f(y)
instead of y = f(x), and we search for dy/dx, we just write:

dx/dy = 1/(dy/dx)

4. Exercise

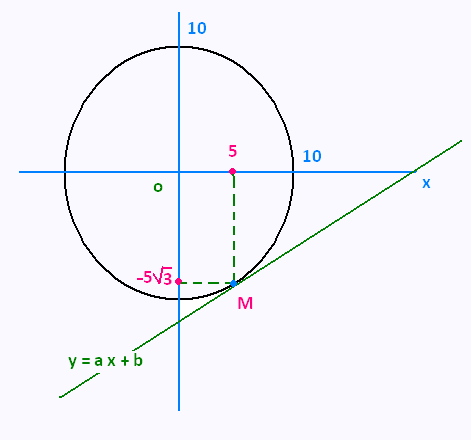
Find the equation of the tangent line to the following circle:

x2 + y2 = 100
at the point (+5, - 5√3).

Hint:

. Calculate dy/dx
. Use the point y(5) = - 5√3