Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
| Calculus I: The derivative : applications
The derivative of a function tells us about some features of its graph. In its domain, the derivative shows whether It is
increasing (goes up) or decreasing (goes down), what are its relative and absolute extrema, and whether it is convex or concave.
1. Locally increasing or decreasing functions
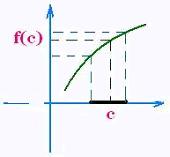
A function f is increasing at the point x = c , where c is
in the domain of the function f, if it exists
a neighborhood around the point c such as:
For any point in the neighborhood , we have:
f(x) < f(c) for x < c, and
f(x) > f(c) for x > c
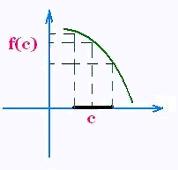
A function f is decreasing at the point x = c , where c is
in the domain of the function f, if it exists
a neighborhood around the point c such as:
For any point in the neighborhood, we have:
f(x) > f(c) for x < c, and
f(x) < f(c) for x > c
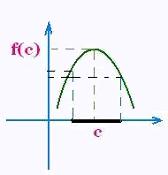
A function f has a relative maximum f(c) at the point x = c , where c is
in the domain of the function f, if it exists
a neighborhood around the point c such as:
For any point not equal to c in the neighborhood, we have:
f(x) < f(c)
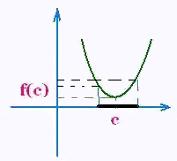
A function f has a relative minimum f(c) at the point x = c , where c is
in the domain of the function f, if it exists
a neighborhood around the point c such as:
For any point not equal to c in the neighborhood, we have:
f(x) > f(c)
2. Increasing or decreasing functions
on an interval
A function f increases on an interval I if:
f(x2) >= f(x1) or any x1 and x2 in the interval where
x2 > x1.
If f(x2) > f(x1), the function is said to be strictly increasing.
Conversely, a function decreases on an interval I if
f(x2) <= f(x1)
for all x2 > x1.
If for all x2 > x1, f(x2) < f(x1), the function is said to be strictly decreasing.
3. Locally Increasing or decreasing functions
and derivative
If the function f is differentiable at the point x = c
If f'(c) > 0 then the function is increasing,
If f'(c) < 0 then the function is decreasing.
4. Increasing or decreasing functions
and derivative on
an interval
If the function f is differentiable on an interval I
For every x in the interval I:
If f'(c) > 0 then the function is increasing on I,
If f'(c) < 0 then the function is decreasing on I.
5. Critical point of a function
A critical point of a function is any value in its
domain where either:
The derivative of the function is 0, or
The function is not differentiable.
That is , if c is a critical point of the function f, then
f'(c) = 0 or f'(c)
The corresponding value of the function at a critical point
is the critical value of this function.
That is , if c is a critical point of the function f, then
f(c) is the critical value of this function.
If f(c) is an extremum of the function f, then c is
a critical point. But the reverse is not true.
Let f a function and c a critical point of f between a and
b such as:
a < c < b
f is continuous on the interval ]a, b[, and
c is the only critical number on the interval [a, b].
If f'(a) > 0 and f'(b) < 0 then f(c) is a relative
maximum.
If f'(a) < 0 and f'(b) > 0 then f(c) is a relative
minimum.
|
|

