Calculus I:
Derivatives
Elasticity
Price Elasticity of Demand

1. The percentage change

The percent change in a variable X is defined as:

Percent change in X =
Change in the variable /Original value of X

That is, if a variable X changes from a value X to another value X + ΔX, then:

Change in the variable = (X + ΔX) - X = ΔX

Percent change in X = ΔX/X

2. Elasticity

We use derivatives to compute elasticity.

In economics, the term elasticity refers to the responsiveness of an economic variable to changes in another economic variable.

The elasticity is measured in terms of percentage changes instead of absolute changes. This means we measure the change in a variable as a percentage of the original amount of the variable.

The elasticity of Y with respect to X is the ratio of the percentage change in Y to the percentage change in X.

Elasticity of Y with respect to X =
Percent change in Y / Percent change in X

The most common use of elasticity in economics is price elasticity of demand or elasticity of demand with respect to price.

3. Price elasticity of demand

The price elasticity of demand is the elasticity of demand ( Y ) with respect to price (X ).

This notion allows us to analyse the responsiveness of the consumer demand for some product or service to changes in the price of that product or service.

If the price changes how will this effect the quantity sold ?

For example, If the price of a book were to increase from 100 $ to 120 $, this would effect the quantity sold to dropp from 50 to 45 per day. The elasticity of demand with respect to the price is E = ((45 - 50)/50)/((120 - 100))/100 = (- 0.1)/(0.2) = - 0.5

If the relationship between demand and price is given by a function Q = f(P) , we can utilize the derivative of the demand function to calculate the price elasticity of demand.

If the change in price passes from P to P + ΔP, and the corresponding change in demand (quantity) from Q to Q + ΔQ, , the corresponding percent changes in price is ΔP/P and corresponding percent changes in demand is ΔQ/Q. So the price elasticity of demand is:

E = (ΔQ/Q)/(ΔP/P) = (P/Q) . (ΔQ/ΔP)

E = (P/Q) . (ΔQ/ΔP)

The factor ΔQ/ΔP represents the average rate of change of demand Q with respect to price P. If we assume the change in price is small, we can replace the average rate of change with the instantaneous rate of change, dD/dP .

If E < - 1 , then demand is elastic and a percent increase in price yields a larger percent decrease in demand.

If - 1 ≤ E ≤ 0 , then demand is inelastic and a percent increase in price yields a smaller percent decrease in demand.

If E = - 1, then the demand is unit-elastic and a percent increase in price yields the same percent decrease in demand.

Demand is perfectly elastic if any increase in price causes the quantity demanded to decrease to 0.

Demand is perfectly inelastic if and increase or decrease in price makes no change in the quantity demanded.

4. Elasticity and total revenue

The revenue is equal to the product of the price per unit ( P ) and the quantity demanded ( Q ) : R = P . Q

If the quantity demanded decreases as the price is increased, what will be the overall effect on the total revenue?

Generally, when the price increases, the demand decreases.

Therefore, the price elasticity of demand changes as the price increases.

For lower prices, the price elasticity of demand is between - 1 and 0 and increasing the price increases revenue.

For higher prices, the elasticity is more negative than 1 and increasing the price leads to lower revenue.

The highest revenue occurs when the elasticity is equal to -1.

So should prices be increased?

1. If demand is inelastic (- 1 ≤ E ≤ 0), then a price increase yields an increase in total revenue.

2. If demand is elastic (E < - 1) , then a price increase yields a decrease in total revenue.

3. Total revenue is highest at a price where demand is unit-elastic. (E = - 1)


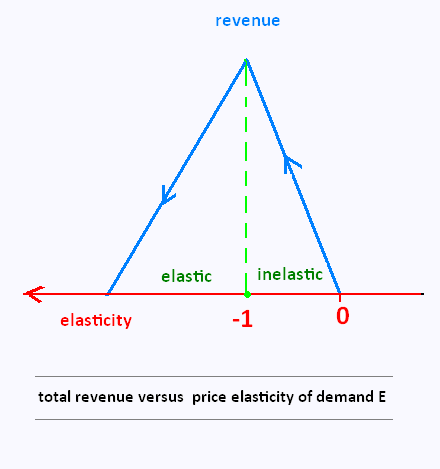
For inelastic demand, price increases are countered by small decreases in the quantity resulting in more revenue. However, when demand is elastic, price increases lead to large drops in the quantity sold that lowers the overall revenue. If maximizing revenue is the overall goal, setting the price where the price elasticity of demand is equal to - 1 is ideal. This goal ignores cost and should be approached cautiously.