Calculus I: Graphing a function

Let f a function. To study f, we proceed by the following steps:

Find the domain of the function,

Set the continuity of this function,

Determine the parity of the function,

Determine its asymptotes,

Derive is f(x) and determine the critical numbers and the relative extrema of the function.

Set f"(x) and the numbers of transition and the inflection points.

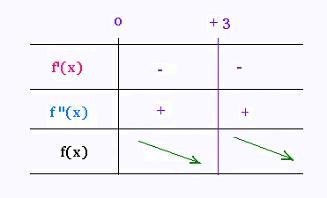
Construct the sign-variation table of the function including the variation of f and its concavity.

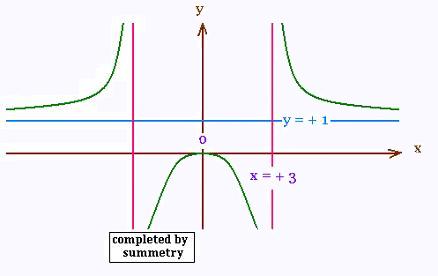
Draw the graph.

f(x) = (x² + 3)/(x² - 9)

Domain D = R / {- 3, + 3}
f is discontinuous at x = - 3 and x = + 3,

lim f(x) = 12/0^- = - ∞
x → - 3^-

lim f(x) = 12/0⁺ = + ∞
x → - 3⁺

lim f(x) = 12/0^- = - ∞
x → + 3^-

lim f(x) = 12/0⁺ = + ∞
x → + 3⁺
f is even because f(- x) = f(x)
The interval of symmetry is [0, + ∞[
The asymptotes are:

Vertical: x = - 3 and x = + 3

Horizontal:
lim f(x) = lim (x²/x²) = 1
x → ± ∞
f'(x) = - 24 x /(x² - 9)² x = 0 f(0) = - 1/3
x = 0 exists in the domain D. So this point is a critical point. The point (0, - 1/3) is an extremum.
f"(x) = (72 x² + 216)/(x² - 9)³
f"(x) = 0 has no solutions. So there are no numbers of transition or inflection points.
f "(0) = 216/(- 9)³ < 0 . So the point x = 0 is a relative maximum of f and the concavity is downward (convex).

A homographic function f is defined as:

f(x) = (ax + b)/(cx + d)
where a, b, c, and d are real constants.

D = R \ {- d/c}
f is discontinuous at x = - d/c
lim f(x) = 12/0^± = ± ∞
x → (- d/c)^±

The line x = - d/c is a vertical asymptote.

lim f(x) = a/c
x → ± ∞

The line y = a/c is a horizontal asymptote.
The function is neither even nor odd, so we study the function in the whole domain D.
There is no oblique asymptote because the function has already a horizontal asymptote.
f '(x) = (ad - bc)/(cx + d)² has no solutions.
So no critic points, then no relative extrema.

The function is increasing if (ad - bc) >0, and decreasing if (ad - bc) <0.
f"(x) = - 2 c (ad - bc)(cx + d)/(cx + d)⁴
f"(x) = o when x = - d/c
This point x = - d/cD, so it is not a transition number, then not an inflection point.

Using the division of polynomials, we can write:
f(x) = (ax + b)/(cx + d) = (a/c) + (1/c)(bc - ad)/(cx + d)
and we see y = a/c is a particular oblique asymptote, that is a horizontal asymptote.

We can also remark that this function f(x) is transformed by a translation from the function f_o(x) = 1/x, with (a/c) vertically, and (- d/c) horizontally. Hence the word homograph i.e. same graph.
Construct the sign-variation table of the function including the variation of f and its concavity.
Draw the graph.