Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
|
Calculus I: Limits
The concept of limit
1. Limits: Intuitive approach and definitions
Using a calculator
Let a function f defined as
f(x) = 2 x + 3
We want to study the behavior of the images of
this function for the values of x close to the value 1.
We have the following two cases:
x approaches 1 from the left:
| x → 1 | f(x) |
| 0.5 | 4.0 |
| 0.77 | 4.54 |
| 0.85 | 4.70 |
| 0.955 | 4.91 |
| 0.999 | 4.998 |
As the variable x takes values close to 1
(while remaining less than 1), the related
images of the function f approach the value 5.
We say that when the value of
variable x approaches 1 by the
left, the images become close to the value 5.
In a more concise manner, we write:
lim f(x) = 5
x → 1-
x approaches 1 from the right:
| 1 ← x | f(x) |
| 1.75 | 6.50 |
| 1.50 | 6.00 |
| 1.2 | 5.40 |
| 1.05 | 5.10 |
| 1.005 | 5.01 |
Similarly, the more the variable x takes
values close to 1 (while remaining greater than 1),
the more the related images of the function f approach
the value 5.
We say that when the value of the variable x
approaches 1 from the right, the function takes values
close to the value 5.
In a more concise, we write:
lim f(x) = 5
x → 1+
We have:
lim f(x) =
x → 1-
| lim f(x) = 5
x → 1+ |
Where in both cases, the value obtained is the same,
we write:
lim f(x) = 5
x → 1
Therefore:
lim f(x) = b
x → a
|
| if and only if | |
lim f(x) = b
x → a-
and
lim f(x) = b
x → a+
|
a and b are real.
Recall then:
a) If
lim f(x) ≠
x → a-
|
lim f(x)
x → a+ |
Then
lim f(x) does not exist.
x → a
b)
If
lim f(x) doesn't exist OR
x → a-
|
lim f(x) doesn't exist
x → a+ |
Then
lim f(x) does not exist.
x → a
2. Examples
2.1. Example 1
Let f a function defined as:
f(x) = (√x - 2)/(x - 4)
We want to know the following;
a)
lim f(x)
x → 4
b)
lim f(x)
x → 0
c)
lim f(x)
x → 1
d)
lim f(x)
x → +∞
a)
lim f(x)
x → 4-
| x → 4 | f(x) |
| 3.05 | 0.26 |
| 3.40 | 0.26 |
| 3.0 | 0.26 |
| 3.80 | 0.253 |
| 3.998 | 0.250 |
lim f(x)
x → 4+
| 4 ← x | f(x) |
| 5 | 0.236 |
| 4.75 | 0.239 |
| 4.20 | 0.247 |
| 4.01 | 0.249 |
| 4.005 | 0.250 |
We have then:
lim f(x) = 0.25
x → 4-
lim f(x) = 0.25
x → 4+
So
lim f(x) = 0.25
x → 4
b)
lim f(x) doesn't exist
x → 0-
lim f(x) = 5
x → 0+
so
lim f(x) doesn't exist.
x → 0
c)
lim f(x) =
x → 1-
| lim f(x) = 1/3
x → 1+ |
so
lim f(x) = 1/3
x → 1
d)
lim f(x) = 1/2
x → +∞
2.2. Example 2
f(x) = (x2 - 9)/(x - 3)
lim f(x) =
x → 3-
| lim (x + 3) = 6
x → 3- |
lim f(x) =
x → 3+
| lim (x + 3) = 6
x → 3+ |
Therefore:
lim f(x) = 6
x → 3
3. Exercises
3.1 Graph the following functions and use those graphs to
determine the related limits:
a)
f(x) = 2/(x - 3)
lim f(x)
x → 3+
lim f(x)
x → 3-
lim f(x)
x → 3
b)
f(x) = (x2 - 16)/(x + 4)
lim f(x)
x → 4+
lim f(x)
x → 4-
lim f(x)
x → 4
3.2. Determine the following limits:
c)
f(x) = (2 - x)1/2
lim f(x)
x → 2+
lim f(x)
x → 2-
lim f(x)
x → 2
d)
f(x) = |x - 7| - 1
lim f(x)
x → 7+
lim f(x)
x → 7-
lim f(x)
x → 7
e)
f(x) = x2 - 1 if x > 0
f(x) = x + 1 if x < 0
lim f(x)
x → 0+
lim f(x)
x → 0-
lim f(x)
x → 0
3.3. For each of the graphed function, determine the
following limits:
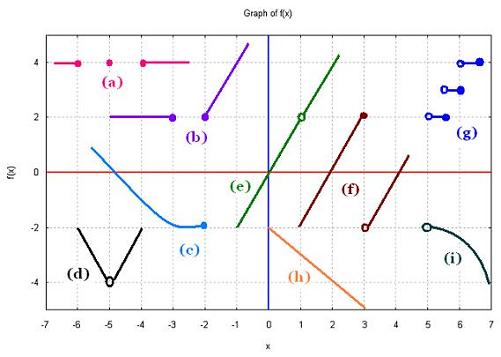
(a)
lim f(x)
x → - 5
(b)
lim f(x)
x → - 3
(c)
lim f(x)
x → - 2
(d)
lim f(x)
x → - 5
(e)
lim f(x)
x → + 1
(f)
lim f(x)
x → + 3
(g)
lim f(x)
x → + 5.25
(h)
lim f(x)
x → + 1
(i)
lim f(x)
x → + 5
|
|

