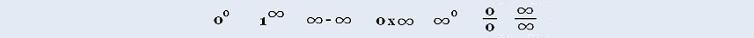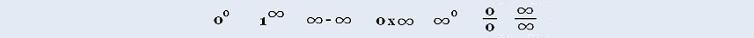Calculus I: Limits
Undetermined forms
1. The 7 undetermined forms
0/0, ∞/∞, ∞ - ∞,
0 x ∞, 1 ∞, 00,
∞0.
When we get one of the above form, we have
to transform the expression of f(x) to evaluate
its limit.
2. The form 0/0
2.1 Example:
lim (x2 - 25)/(x + 5)) = 0/0
x → - 5
Transforming f(x) gives:
(x2 - 25)/(x + 5)) = x - 5
Therefore:
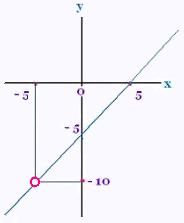
lim (x2 - 25)/(x + 5)
x → - 5
= lim (x - 5) = - 10
x → - 5
|  |
2.2 General rule:
When
lim f(x) = 0/0
x → a
We have necessarily
f(x) = (x - a)g1(x)/(x - a)g2(x)
= g1(x)/g2(x)
Therefore:
lim f(x) =
x → a
| lim g1(x)/ g2(x) which is ≠ 0/0
x → a
|
3. The form ∞/∞
3.1 Example:
lim (3x2 + 1)/(x2 + 5) = ∞/∞
x → + ∞
Transforming f(x) gives:
(3x2 + 1)/(x2 + 5) = (3x2 + 1)/x2/(x2 + 5)x2 =
(3 + 1/x2)/(1 + 5/x2)
Therefore:
lim (3x2 + 1)/(x2 + 5) =
x → + ∞
|
lim (3 + 1/x2)/(1 + 5/x2) = 3/1 = 3
x → + ∞
|
3.2. General rule:
When
lim f(x) = ±∞ /±∞
x → ±∞
We have necessarily a polynomial function of the
form :
f(x) = g1(x)/g2(x).
We divide the numerator and denominator by the
variable with the largest exponent.
Therefore:
lim f(x) =
x → ±∞
|
lim g1(x)/g2(x)
x → ±∞
|
which is ≠ ∞/∞
3.3 Other example:
f(x) = (x + 3 )/(x2 - 1)
lim f(x) = - ∞/+∞
x → - ∞
= lim (x + 3)/x2/(x2 - 1)/x2
x → - ∞
= lim (1/x + 3/x2)/(1 - 1/x2)
x → - ∞
= (0 + 0)/(1 - 0) = 0
4. The form ∞ - ∞
4.1 Example 1 :
f(x) = x2 - x
x → ∞
lim f(x) = ∞ - ∞ : undetermined.
x → ∞
We factor using the term of the greatest degree:
x2 - x = x2(1 - 1/x)
Therefore:
lim f(x) = ∞( 1 - 0) = ∞
x → ∞
The rule is:
For a polynomial function, we take just the term
of the greatest degree.
4.2 Example 2:
f(x) = 3 x4 - x2 + 4
x → - ∞
lim f(x) = ∞ - ∞ : undetermined.
x → ∞
We use just the term of the greatest degree:
Therefore:
lim f(x) = lim 3 x4 = + ∞
x → ∞
4.3 Example 3:
f(x) = √x - x
x → +∞
lim f(x) = ∞ - ∞ : undetermined.
x → + ∞
We use the conjugate quantity of f(x):
Therefore:
f(x) = √x - x = (√x - x)((√x + x)/(√x + x) =
(x - x2)/(√x + x) = x (1 - x)/(√x + x) =
Dividing the numerator and denominator by x gives:
f(x) = (1 - x)/((√x)/x + 1)
We have (√x)/x = √x/x2 = √(1/x)
Therefore:
f(x) = (1 - x)/(√(1/x) + 1)
So
lim f(x) = - √/(0 + 1) = - ∞
x → ∞
5. The form 0 x ∞
5.1 Example 1 :
f(x) = x3 . 2/(x2 - 1) = 0 x ∞ : undetermined.
x → 0
Rule:
We use one of the above transformation.
x3 . 2/(x2 - 1) = 2 x3/(x2 - 1)
We divide the numerator and denominator by x3, that
gives:
f(x) = 2 /(x - 1/x3)
Therefore:
lim f(x) = 2/(0 - ∞ ) = 0
x → 0
The rule is:
Use one of the above transformation.
4.2 Example 2:
f(x) = |x - 2|/(x - 2)
x → 2;
lim f(x) = 0 x ∞ : undetermined.
x → 2
We have:
|x - 2| =
x - 2 if x > 2
- (x - 2) if x < 2
Therefore:
lim f(x) = (x - 2)/(x - 2) = 1
x → 2+
And
lim f(x) = - (x - 2)/(x - 2) = - 1
x → 2-
So
lim f(x) 
x → 2
3. Exercises
1) 0/0
a)
lim (x2 - 6x + 8)/(2x2 - 3x - 2)
x → 2
b)
lim (2 - (x - 3)1/2)/(x2 - 49)
x → 7
c)
lim (x4 - 1)/((3 - x)1/2 + 2x)
x → - 1
d)
lim (3 - (x + 1)1/2)/(√x - 2√2)
x → + 8
e)
lim (3 + x )/( 1 + (3/x))
x → - 3
2) ∞/∞
a)
lim (3 + x )/(1 + x)
x → + ∞
b)
lim (4x3 - 2 x + 7)/(3x3 + 1)
x → + ∞
c)
lim (x2 + 7)/(x3 + 4)
x → - ∞
d)
lim (x + 1)/(2x3 - √(x2 - 2))
x → - ∞
e)
lim (x - 1)/(√(2x) + √(x)
x → + ∞
f)
lim (x2 + 2x)/(x + √(x2 - 1)
x → - ∞
3) ∞ - ∞
a)
lim (2x4 - x + 5)
x → + ∞
b)
lim (√(x2 + x) - x)
x → + ∞
c)
lim (x + √(2x2 + x - 1))
x → - ∞
d)
lim (1/x3 - 1/x)
x → 0
4) 0 x ∞
a)
lim (x(1/x - 1/(x - 1)))
x → + ∞
b)
lim ((1/(x - 3)3) (1/x - 1/3)) )
x → + 3
c)
lim (x √(1 + 1/x))
x → 0+;
d)
lim x/√(x)
x → + ∞
|