Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
|
Calculus I: Marginal analysis
The marginal analysis is the examination of the
situation when we add one unit as a independent
variable to the system.
In other words, it is a technique that allows to study the effect on a function f(x) (cost, production, income, ...) by a unit increase in its independent variable (x).
In economics, the marginal analysis identifies the effect (benefits or costs) on total revenue or cost caused by a marginal or incremental change (a unit change) to given resources.
This technique is well explained by derivative.
1. Definitions
The marginal analysis involves the marginal cost
which is the the derivative of the function of the related
situation.
The marginal cost for the function f(x) is
(f(x+1) - f(x))/((x + 1) - x) =
(f(x+1) - f(x)) ≈ f '(x) at the point x
2. Example
A student spends: E (x) = x + (x/2)2 kilo dollars
for x terms for the related school fees.
At the present time, it has been taken 10 semesters.
The cost for these ten terms is:
E(10) = 10 + 52 = 35 k$
The cost of the fees, if the student takes an
extra term (11th term) will be: E(10 + 1) - E(10).
E(x + 1) - E(x) = x + 1 + ((x+1)/2)2 -
x - (x/2)2 =
1 + (x/2)2 + x/2 + (1/2)2
- (x/2)2 =
1 + x/2 + 1/4 = (5/4) + x/2
E(x + 1) - E(x) = (5/4) + x/2
Therefore
The cost for the 11th term is:
E(0 + 1) - E(10) = (5/4) + 10/2 = 25/4 = 6.25 k$
If we use the definition of the marginal cost
we will have :
(E(x+1) - E(x))/((x + 1) - x) =
(E(x+1) - E(x)) ≈ E'(x) at the point x = 10.
E'(x) = (x + (x/2)2)' = 1 + (1/2)2(x/2) =
1 + x/2.
At the point x = 10, we obtain the marginal cost:
E'(10) = 1 + 10/2 = 6.00 k$
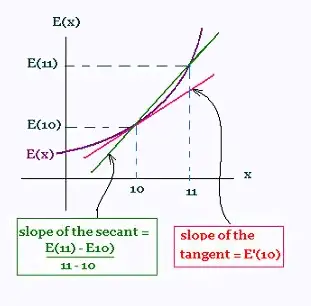
From the following graph, we understand the difference between the two values.
The first expression:
(E(x+1) - E(x)) represents the slope of the secant, and the
second expression which is the derivative E'(x) of the function E(x)
represents the slope of the tangent at the point x = 10.
3. Marginal analysis formulas

|
|

