Calculus I: Derivative
Marginal analysis
1. Marginal analysis
It is about some applications of derivatives in the business world.
Marginal analysis is used to estimate the amount of the change
in a function from the next item.
This function is either cost ,
revenue or profit.
2. Marginal of a function
Marginal of a function is the derivative of this function; that
is the rate of increasing or decreasing of the related production:
Marginal function of f(x) = f'(x)
The exact or actual function is the difference between
the function of the (x + 1)th item and the xth item: :
Exact function is Δf(x) = f(x + 1) - f(x)
Using the definition of the derivative:
lim f(x + h) - f(x)/h = f'(x),
h → 0
an approximation, with h ≈ 1, of this
marginal cost gives:
f'(x) = df(x)/dx ≈ f(x + 1) - f(x)/1
= f(x + 1) - f(x) = Δf(x)
The marginal value of f(x) for the (x + 1)th
unit is f'(x).
The actual value of f(x) for the (x + 1)th
unit is f(x + 1) - f(x)
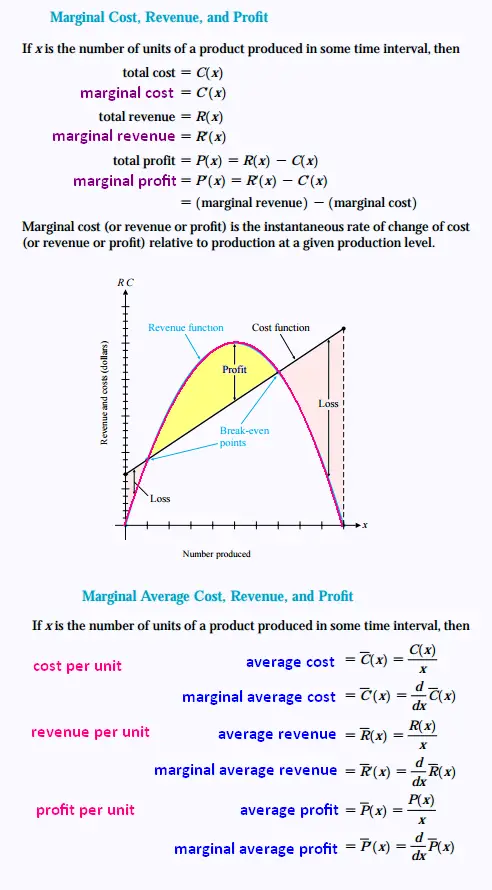
3. Formulas
• Marginal function = f'(x)
• Exact or actual function is Δf(x) = f(x + 1) - f(x)
• Total function = variable function + fixed value
• Average function = f(x)/x
This function is either cost ,
revenue or profit.
• x is the number of items quantity
• Total cost = variable cost + fixed cost
• The demand function p(x) is
the unit price
function.
It might depend on x.
The revenue function R(x), that is how much money is made by
selling x items, is:
R(x) = x . p(x)
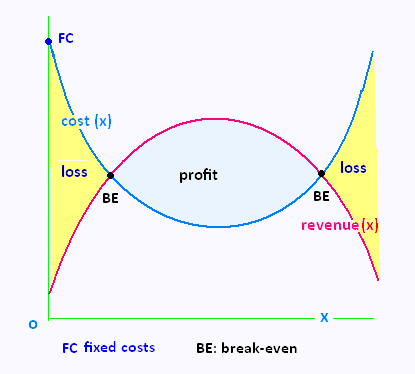
• For x items produced and sold , we always have:
Profit(x) = Revenue(x) - Cost (x)
• The break-even points are the intersection points where total revenue equals total cost.
There are always somme fixed costs, such as the rent of factory,
pay people, even if we produce nothing.
3. Marginal analysis formulas
4. Example
A compagny produces items to sell and make
profit.
The company has a fixed cost of $4000 and a variable cost
given by:
Cv(x) = 0.3 x2 + 50 x
• The total cost function is:
C(x) = Cv(x) + 4000 = 0.2 x2 + 50 x + 4000
C(x) = Cv(x) + 4000 = 0.2 x2 + 50 x + 4000
• The marginal cost when x = 500 is
C'(x = 500)
We have
C'(x) = 0.4 x + 50
So C'(x = 500) = 0.4 (500) + 50 = 250 $
This marginal cost is an estimate of the cost of producing
the 501st item.
The demand function p(x), that is
the unit price function is given by
x = - 500 + 5 p(x)
From this expression we obtain:
p(x) = 0.2 x + 100
p(x) = 0.2 x + 100
So the revenue function is :
R(x) = x . p(x) = 0.2 x2 + 100 x
R(x) = x . p(x) = 0.2 x2 + 100 x
Therefore the profit is expressed as:
P(x) = R(x) - C(x) =
(0.2 x2 + 100 x) - (0.2 x2 + 50 x + 4000 ) =
0.2 x2 + 100 x - 0.2 x2 - 50 x - 4000 =
50 x - 4000
P(x)= 50 x - 4000
So
P'(x) = 50
• An estimate of the amount of profit from the 301st item (the change
in profit as we go from 300 items to 301 items) is given by:
P'(300) = 50 which is constant.
• The exact change in profit is given by
P(301) - P(300) = (50 (301) - 4000) - (50 (300) - 4000) =
50 (301) - 50 (300) = 50 . 1 = 50
• The average cost function.
C(x) is the cost function for some item then the average
cost function is
 (x) = C(x)/x
= (0.2 x2 + 50 x + 4000
)/x = 0.2 x + 50 + 4000/x (x) = C(x)/x
= (0.2 x2 + 50 x + 4000
)/x = 0.2 x + 50 + 4000/x
 (x) = 0.2 x + 50 + 4000/x (x) = 0.2 x + 50 + 4000/x
|

