Calculus I
Limits
Derivative
Exercices
Applications
Marginal analysis
© The scientific sentence. 2010
|
Calculus I: Sandwich theorem
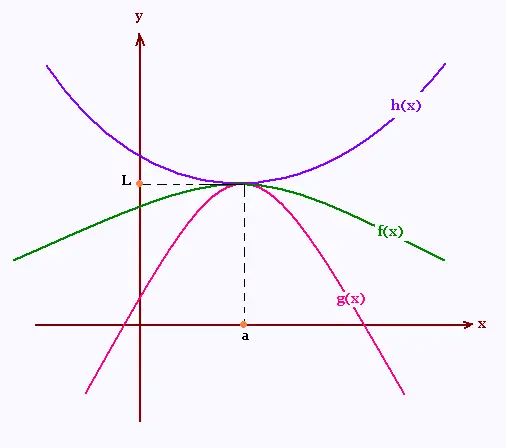
1. Statement
The squeeze theorem, known also as the sandwich theorem or
Pinching theorem is used to evaluate the limit of a function by
comparison with two other functions whose limits are known
or easily calculated.
Let I be an interval having the point "a".
Let f, g, and h be functions defined on I, except possibly at "a".
For every x in I not equal to a, if we have:
When the limits on the upper bound and lower
bound are the same, then the function in the
middle is squeezed into having the same limit.
|
2. Examples
Example 1
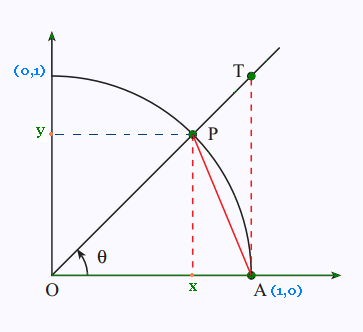
We'll use the Squeeze theorem by establishing upper
and lower bounds on sin(x)/x in an interval around 0;
Note the two functions cos(x) and sin(x)/x are even.
Thus, we'll
just establish le bounds on the interval (0, π/2).
Let's compare the areas:
area of triangle POA ≤ area of sector POA ≤ area of triangle TOA.
That is:
sin(x)/2 ≤ x/2 ≤ tan(x)/2
2/sin(x) is positive. Hence:
1 ≤ x/sin(x) ≤ 1/cos(x)
so
Now let's take the limit:
cos(x) = cos(0) = 1, by continuity of cosine.
Hence
Example 2
Example 3
Example 4
|
|

