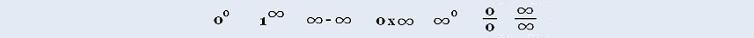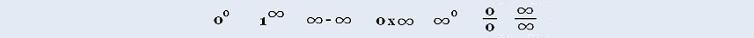Calculus I: Trigonometric functions
Derivative

1. Derivative of trigonometric functions

1.1. Definitions

1.

d(sin x)/dx =

lim (sin(x + Δx) - sin x)/Δx
Δx → 0

We have:

sin(x + Δx) = sin x cos Δx + cos x sin Δx
sin(x + Δx) - sin x =
sin x (cos Δx - 1) + cos x sin Δx

Therefore

d(sin x)dx =
lim (sin x (cos Δx - 1) + cos x sin Δx)/Δx
Δx → 0
=
lim (sin x (cos Δx - 1))/Δx + lim (cos x sin Δx)/Δx
Δx → 0
=
(sin x ) lim (cos Δx - 1))/Δx + (cos x) lim sin Δx)/Δx
Δx → 0
=
(sin x ) (0) + (cos x ) (1) = cos x
Δx → 0

Hence:

d(sin x)/dx = cos x

Proof: see exercises section.

2.
d sin (f(x))/dx

Let y = sin u with
u = f(x)

The derivative chain rule is written as:

dy/dx = (dy/du)(du/dx)

That is:

dy/dx = (d (sin u)/du)(f'(x))
= cos u . f'(x) = (cos f(x)) . sin (f(x))/dx

Hence:

d sin (f(x))/dx = (cos f(x)) . d(f(x))/dx

3.
We have also:

d cos (f(x))/dx = - (sinf(x)) . d(f(x))/dx = - f'(x) . sin f(x)

1.2. Examples

a)
d sin (3 x + 1)/dx = d sin (f(x))/dx =
(cos (3 x + 1)) . (3 x + 1)' =
(cos (3 x + 1)) . (3) = 3 cos (3 x + 1)

b)
cos²y = 2y + sinx

2 (cos y) (- sin y) (dy/dx) = 2(dy/dx) + cos x
- 2 sin y cos y (dy/dx) = 2(dy/dx) + cos x
- 2 (dy/dx) (sin y cos y + 1) = cos x
2 (dy/dx) (sin y cos y + 1) = - cos x /2(sin y cos y + 1) =
- cos x /(sin (2y) + 2)

2. Example of trigonometric function

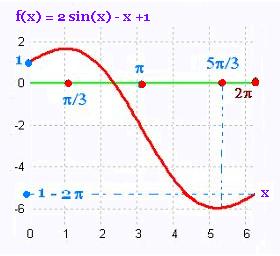
Let f(x) = 2 sin x - x + 1

a)
Domaine is D = R.
We study this function in the interval I = [0, 2π]

b)
f'(x) = 2 cos x - 1
f'(x) = 0
cos x = 1/2
The critic numbers are {π/3, 5π/3}

f '(x) > 0 → cos x > 1/2 → - π/3 < x <π/3 → (x <π/3 and x > 5π/3)
so in the interval ]0,π/3[ ∪ ]5π/3, 3π[, the function increases.

c)
f''(x) = - 2 sin x
f''(x) = 0
sin x = 0
The transition numbers are {0, π, 2π}
They are inflection points.

d) Since the interval of the study of the function is [0, 2π], the horizontal and oblique asymptotes are not considered. In addition, the function is not discontinuous at any point in I (and R), so the verical asymptote are not considered.

3. Inverse trigonometric function: Derivative

3.1. Derivative of ArcSin(x)

Let:
y = g(x) = arcsin x
defined by
x = sin y and
- π/2 <= y <= +π/2

f(g(x)) = sin [ArcSin(x)]

(d sin y/ dy ) . (d Arcsin x /dx) = dx/dx = 1
(cos y) . d Arcsin x)/dx = 1

d(Arcsin x)/dx = 1 /cos y = 1/(1 - sin²y)^1/2 = 1/(1 - x²)^1/2

3.2. Derivative of ArcCos(x)

Let:
y = arccos x
defined by
x = cos y and
0 <= y <= +π

1 = dx/dx = d(cos y)/dy . dy/dx =
(- sin y) . d(arccos x)/dx

Therefore:

d(arccos x)/dx = - 1/sin y =
- 1/(1 - cos²y)^1/2 = - 1/(1 - x²)^1/2

3.3. Derivative of ArcTan(x)

Let:
y = arctan x
defined by
x = tan y and
- π/2 < y < +π/2

1 = dx/dx = d(tan y)/dy . dy/dx =
(1/cos²(y)) . d(arctan x)/dx

Therefore:

d(arctan x)/dx = cos²(y) =
= 1/(1 + tan²y) = 1/(1 + x²)

3.4. Derivative of ArcCot(x)

Let:
y = arccot
defined by
x = cot y and
0 < y < +π

1 = dx/dx = d(cot y)/dy . dy/dx =
- (1 + cot² y) . d(arccot x)/dx

Therefore:

d(arccot x)/dx = - 1/(1 + cot²y) = - 1/(1 + x²)

3.5. Derivative of arcsin (f(x))

Let:
y = arcsin u
with u = f(x)
The chain rule derivative is written as:

dy/dx = dy/du . du/dx
1/(1 - u²)^1/2 . df(x)/dx =
1/(1 - f(x)²)^1/2 . df(x)/dx

Similarly, we have:

3.6. Other trigonometric function: Derivative

3.6.1. sec(x) and arcsec(x)

By definition:

sec(x) = 1/cos(x)

d sec(x)/dx = sin(x)/cos²(x)

d csc(x) /dx = - cos (x) /sin²(x)

Let:
arcsec(x) = y
sec(y) = x

1 = dx/dx = d(sec(y))/dy . dy/dx
dy/dx = 1/d(sec(y))/dy
= 1/sin(y)/cos²(y) = cos²(y)/sin(y)
= (1/sec²(y)) . 1/[1 - cos²(y)]^1/2
(1/xsup>2) . 1/[1 - (1/sec)²(y)]^1/2 =
(1/xsup>2) . 1/[1 - (1/x)²]^1/2 =
1/x [x² - 1]^1/2

Therefore:
d(arcsec(x))/dx = 1/x(x² - 1)^1/2

3.6.2. csc(x) and arccsc(x)

By definition:

csc(x) = 1/sin(x)

4. Exercises

a) f(x) = cos x
we want to prove that d(cosx)/dx = - sin x.

b) f(x) = cos ( 3 x² + 1)
Determine df(x)/dx.