Calculus II: Riemann sum & integrals

1. Riemann sum

1.1. Definition

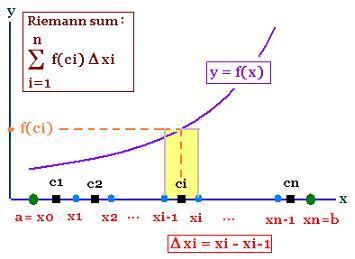
Let f a function continue on the interval [a,b].
We want to construct a sum of the function f as follow:

1. We subdivide the interval [a, b] into n sub-intervals and obtain the partition of this interval:
[x0 = a, x1], [x1, x2], [x2, x3], ..., [xi-1, xi], ..., [xn-1, xn].
The width of each sub-interval is equal to Δxi = xi - xi-1.

2. We choose a representative point ci inside each sub-interval: ci ∊ [xi-1, xi]

3. We perform the sum:
f(c1)Δx1 + f(c2)Δx2 + ... + f(ci)Δxi + ... + f(cn)Δxn =
Σ_i=1ⁿf(ci)Δxi

This sum is called Riemann sum or integral sum of the function f on the interval [a, b].

1.2. Example

What is the value of the Riemann sum of the function f(x) = x² + 1 on the interval; [2, 7]?

Let consider 5 sub-intervals with equal width Δxi equal to 1; and the mid-point of each sub-interval as its representative. Therefore

The partition is:
[x0 = 2, 3], [3, 4], [4, 5], [5, 6], [6,7]

The 5 representatives ci are:
2.5, 3.5, 4.5, 5.5, 6.5

The Riemann sum is:

Σ_i=1⁵ f(ci)Δxi =
f(2.5)(1) + f(3.5)(1) + f(4.5)(1) + f(5.5)(1) + f(6.5)(1). =
((2.5)² + 1) + ((3.5)² + 1) ((4.5)² + 1) ((5.5)² + 1) ((6.5)² + 1).
= 6.25 + 12.25 + 20.25 + 30.25 + 42.25 + 5 = 116.25

f(x) = x² + 1
Σ_i=1⁵ f(ci)Δxi = 116.25 units².

2. Definite integral

2.1. Definition

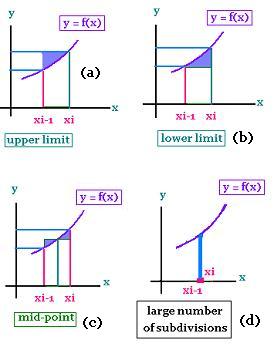
Note that the width of the sub-interval is not necessarily the same for all the intervals of the partition, and the representative point is not necessarily a midpoint.

The width of the sub-intervals are taken equal to make the calculations simple.

If we take the upper bound of the sub-interval instead of the midpoint we will gain the related triangle in each sub-interval (a).

If we take the lower bound of the sub-interval instead of the midpoint we will lose the related triangle in each sub-interval (b).

If we take the mid-point of the sub-interval we gain and loose the two related equal triangle. Therefore , the mid-point as a representative point is a good approximation (c).

The more the width of the sub-interval is small (Δx → 0), the more we approach the true value of the sum. This is obtained by taking a large number of subdivisions (d). In this case the position of the representative does not matter.

f is a function continue on the interval [a, b]

If lim Σ_i=1ⁿ f(ci)Δxi = A
max Δxi → 0

then the function f is integrable on the interval [a, b]. The value A of the limit is the definite integral of the function f on [a, b], denoted by:

	b
∫		f(x) dx
	a

Integral of f(x) dx from a to b.

While Δxi tends to zero, the value A does not depend on the representative within each sub-interval, and does not depend on the subdivision. To calculate the Riemann sum, it is therefore easier to take equal sub-intervals.

We have then: Δxi = (b - a)/n, and the definition of definite integral becomes:

	b						n
∫		f(x) dx	=	limit			Σ	f(ci) Δxi
	a			n → ∞			i=1

2.2. Example

Value of the Riemann integral of f(x) = x² + 1

	7
∫		x2 + 1 dx
	2

The function f(x) is continuous in the interval [2, 7].

We subdivide the interval [2, 7] in n equal sub-intervals of width Δxi = dx = (7 - 2)/n = 5/n.

xo = 2
x1 = xo + 5/n = 2 + 5/n
x2 = x1 + 5/n = 2 + 2(5/n)
x3 = x2 + 5/n = 2 + 3(5/n)
... = ...
xi = b = 2 + i(5/n) = 7

2.2.1. Representative point at the mid-point

The representative points are chosen as the mid-point of sub-intervals:

c1 = (x0 + x1)/2 = (4 + 1 (5/n))/2
c2 = (x1 + x2)/2 = (4 + 3 (5/n))/2
c3 = (x2 + x3)/2 = (4 + 5 (5/n))/2
... = ...
ci = (xi-1 + xi)/2 = (4 + (2i - 1)(5/n))/2 = 2 + (2i - 1)(5/n)
... = ...
cn = (xn-1 + xn)/2

Σ_i=1ⁿ f(ci)Δxi = Σ_i=1ⁿ f(2 + (2i - 1)(5/n))(5/n) =
(5/n) Σ_i=1ⁿ f(2 + (2i - 1)(5/n))

f(2 + (2i - 1)(5/n)) = (2 + (2i - 1)(5/n))² + 1 =
(4 - 10/n) +(20/n - 25/n²)i + (25/n²)i² + 1

Therefore

Σ_i=1ⁿ f(2 + (2i - 1)(5/n))(5/n) =
(5/n) Σ_i=1ⁿ [(4 - 10/n) +(20/n - 25/n²)i + (25/n²)i² + 1] =

Using the formulas: Σ_i=1ⁿ E = n E
Σ_i=1ⁿ i = n(n + 1)/2
Σ_i=1ⁿ i² = n(n + 1) (2n + 1)/6


we obtain:

Σ_i=1ⁿ f(ci)Δxi =
(5/n) [n(4 - 10/n) +(20/n - 25/n²)n(n + 1)/2 + (25/n²)n(n + 1) (2n +1)/6 + n] =
5 [(4 - 10/n) +(20/n - 25/n²)(n + 1)/2 + (25/n²)(n + 1)(2n +1)/6 + n]

Now we evaluate the related limit:

lim Σ_i=1ⁿ f(ci)Δxi = 116.67
n → ∞

Hence

	7
∫		(x2 + 1) dx = 116.67 units2
	2

2.2.2. Representative point at the upper bound

The representative points are chosen as the upper bound of sub-intervals:

c1 = x1 = x0 + 5/n = 2 + 5/n
c2 = x2 = x1 + 5/n = x0 + 2 5/n = 2 + 2 5/n
c3 = x3 = x0 + 3 5/n = 2 + 3 5/n
... = ...
ci = = xi = 2 + 5i/n
... = ...
cn = = xn = 2 + n 5/n = 7


Σ_i=1ⁿ f(ci)Δxi = Σ_i=1ⁿ f(2 + 5i/n)(5/n) =
(5/n) Σ_i=1ⁿ f(2 + 5i/n)

f(2 + 5i/n) = (2 + 5i/n)² + 1 = 5 + 20i/n + 25i²/n²

Therefore

Σ_i=1ⁿ f(2 + 5i/n) (5/n) =
(5/n) Σ_i=1ⁿ [5 + 20i/n + 25i²/n²] =

Using the formulas: Σ_i=1ⁿ E = n E
Σ_i=1ⁿ i = n(n + 1)/2
Σ_i=1ⁿ i² = n(n + 1) (2n + 1)/6


we obtain:

Σ_i=1ⁿ f(ci)Δxi =
(5/n) [5 n + (20/n)n(n + 1)/2 + (25/n²)n(n +1 )(2n + 1)/6] =
5 [5 + (20/n)(n + 1)/2 + (25/n²)(n + 1)(2n + 1)/6]

Now we evaluate the related limit:

lim Σ_i=1ⁿ f(ci)Δxi = 5(5 + 10 + (25)(2)/6] = 116.67
n → ∞

Hence

	7
∫		(x2 + 1) dx = 116.67 units2
	2

4. Exercises