Calculus II: Differentials
1. Differential of a function
Differentiation is an explicite form of a derivative.
If the derivative of function f(x) at the point x is f'(x), we define the differential
of the function f(x) by df(x) such as:
df(x) = f'(x). dx
dx is called the differential element.
This notation of the derivatice is very practical in the calculus
of integrals.
Let increase the variable x by Δx. This generates:
- 1. An increase of its image f(x). f(x) becomes f(x + Δx). The increase in f(x) is:
Δy = f(x + Δx) - f(x)
- 2. An increase of its image, via the tangent line to the curve of f(x) at the point x , by dy. The related rate
dy/Δx is the slope of the tangent that is equal to the derivative of the function at the point x. That is
f '(x) = dy/Δx
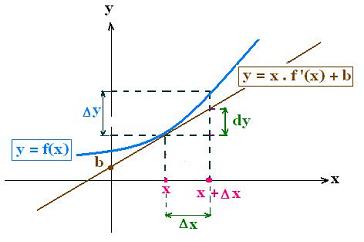
When Δx is small, it becomes dx and
Δy becomes dy.
Therefore, the above
formula becomes:
f'(x) = dy/dx = df(x)/dx
df(x) = f '(x). dx
2. Indefinite Integrals
In Algebra, many functions such as √(x), sin(x), ln(x) ,..
have an inverse function. The derivative function f'(x) has
an inverse function called anti-derivative function. The
antiderivative of f'(x) is the function f(x). We obtain f(x)
by the operation integration of f'(x). This anti-derivative
operation is called also indefinite integral , or
the primitive function.
Given a function f(x), an anti-derivative of f(x)
is the function F(x) such that :
F'(x) = f(x)
.
The expression of a primitive function F(x) of f(x) is:
F(x) = ∫f(x) dx + cst
∫ is called the integral symbol. f(x)
is called the integrand, x the integration variable, and "cst" is
the constant of integration.
3. First rules to integrate functions
There are no general rules, as we have for derivative, to integrate
functions. We use some rules of the derivative to obtain
some primitive of functions.
3.1. Rule to integrate a power (≠ - 1) of a variable
f (x) = xn+1/(n + 1) + Cst
f'(x) = (n + 1)xn/(n + 1) = xn
So
∫ f'(x) dx = f(x) . That is
∫ xn dx = xn+1/(n + 1) + Cst
∫ xn dx = xn+1/(n + 1) + Cst
n≠ - 1
3.2. Rule to integrate a power (= - 1) of a variable
If n = - 1, we have, by definition:
∫ (1/x) dx = ln |x| + Cst
∫ dx/x = ln|x| + Cst
ln is the natural logarithm.
4. Properties of indefinite integral
∫ k. f(x) dx = k ∫ f(x) dx, k is a real constant.
∫ [f(x) ± g(x)] dx = ∫ f(x) dx ± ∫ g(x) dx
There is no rule to integrate a product or division of two functions, as
we have for derivatives.
In most cases, we transform a function to integrate into an
expression to whom we can apply the above rules.
5. Exercises
What are the primitive of the following functions:
a) f(x) = 2 x7
b) f(z) = 5/√z
c) f(t) = ln (t)
d) f(x) = (x4 + 2 x - 4)/x2
e) f(x) = x4 + 2/x
|