Calculus II: Volume of solid of revolution

We have seen that the length of an arc describes by a function f(x) is:

dL = [1 + (f '(x))²] ^1/2 dx

We use this result to determine the lateral area (curved surface) generated by the revolution of a curve around an axis.

1.Lateral area generated by a curve

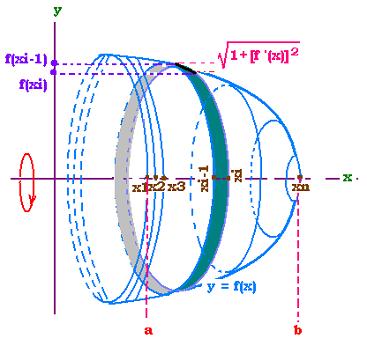
Let f(x) a function continuous on the interval [a, b], and f '(x) its continuous derivative on ]a, b[.

We want to determine the area generated, between x = a and x = b, by the revolution of the curve of f(x) around the x-axis.

Let divide the interval [a, b] in n equal sub-intervals of width Δx2, Δx2, ..., Δxi-1, Δxi, ..., Δxn.

For each point x = xi corresponds its image f(xi) and the elementary arc length ΔLi = [1 + (Δf(xi)/Δxi)²]^1/2, where
Δf(xi) = f(xi) - f(xi-1), and
Δxi = xi - xi-1.

By a revolution around the x-axis the elementary arc length ΔLi generates an elementary lateral area :

ΔAi = ΔLi . 2π f(xi)

The total area A is the sum of the contributions of all the elementary Ai; so

		i = n
A = lim	Σ		Ai
n →+∞		i = 1

=

		i = n
2π lim	Σ		f(xi) [1 + (Δf(xi)/Δxi)2] 1/2
n →+∞		i = 1

=

	x = b
2π ∫		f(x) [1 + (f '(x))2] 1/2 dx
	x = a

2.Example

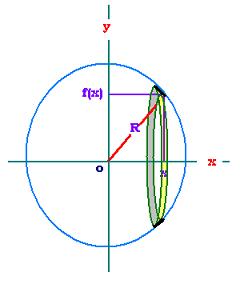
Lateral area of a sphere of radius R centered on the origin.

We determine first the lateral area of a half-sphere generated by the curve of:

f(x) = [R² - x²]^1/2.

around the x-axis between 0 and R.

The function is continuous on [-R, R] then on [0, R]. Its derivative f '(x) is continuous on ]0, R[

f '(x) = - x/[R² - x²]^1/2

dL = [1 + (f '(x))²]^1/2 dx =
= R/[R² - x²]^1/2 dx

Therefore

	x = R
A = 2π ∫		[R2 - x2] 1/2 R/[R2 - x2] 1/2 dx
	x = 0

=

	x = R
2π R ∫		dx
	x = 0

= 2π R²

Hence

The lateral area of a sphere of radius R is 2 x A = 4π R²

5. Exercises