Calculus II:

Definite integral
numerical approaches
Rectangles method

Before integration was developed by Newton and Leibniz, , mainly the Fundamental Theorem of Calculus, the way to find the area under curves ( for example under an arch) is to add areas of rectangles.

Adding rectangles

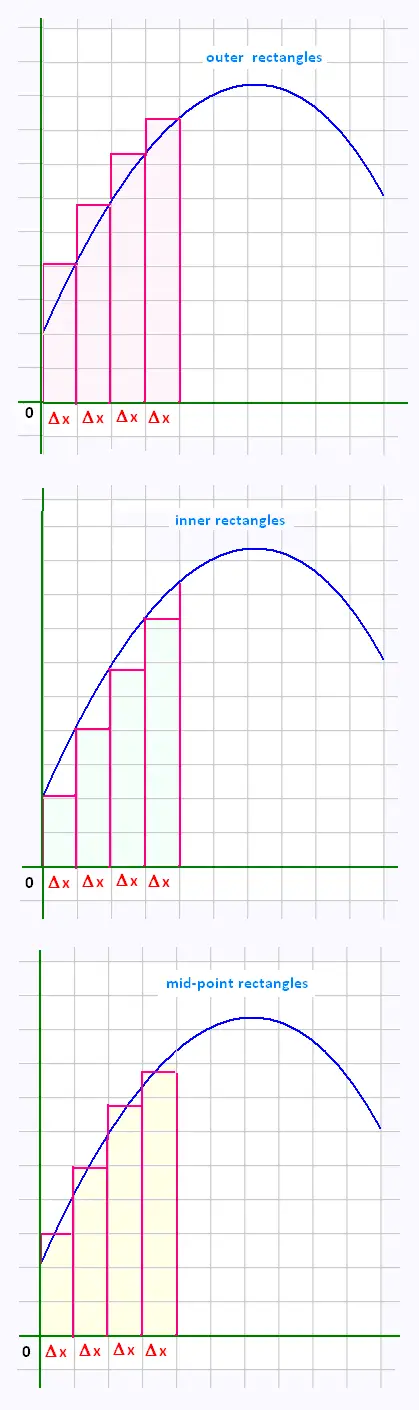
We divide the space under the curve into rectangles and add the areas of those rectangles.

The height of each rectangle is the function value of each corresponding width (Δx).

We get a better result if we take more and more rectangles.

In the Rectangles method, we approximate the area using rectangles .

Using rectangles, to calculate the area under the curve, we will consider three cases :

1. Outer rectangles:

We add the areas of the "outer" rectangles:

A = Δx f(Δx) + Δx f(2Δx) + ... + Δx f(3Δx) + Δx f(4Δx).

Generally,

A = Δx f(Δx) + Δx f(2Δx) + ... + Δx f(nΔx)

Δx [f(Δx) + f(2Δx) + ... + f(nΔx) ]



2. Inner rectangles:

We add the areas of the "inner" rectangles.:

A = Δx f(0) + Δx f(Δx) + Δx f(2Δx) ) + Δx f(3Δx) + Δx f(4Δx)]

Generally,

A = Δx f(0) + Δx f(Δx) + ... + Δx f((n - 1)Δx)

A = Δx [f(0) + f(Δx) + ... + f((n - 1)Δx) ]

3. mid-point rectangles.

A third way of doing this problem would be to find the mid-point rectangles.

A = (Δx/2) f(Δx ) + (3/2)Δx f(2Δx) + (5/2)Δx f(3Δx) + (7/2)Δx f(4Δx)

Generally,

A = (Δx/2) f(Δx ) + (3/2)Δx f(2Δx) + (5/2)Δx f(3Δx) + ... + (n - 1/2)Δx f(nΔx)