Calculus II: Sequences

1. Introduction

A sequence is a list of real numbers written in a specific order. The list can have finite or infinite number of terms. In general, we deal with infinite sequences.

Example:

The sequence:

2, 5, 10, 17, ..., a_n, ... is an infinite sequence.

a₁ = 2 is the first term,
a₂ = 5 is the second term,
...
a_n the nth term. It is called general term of the sequence.

Explicitly, in this example: a_n = n² + 1


We denote a sequence as :

{a₁, a₂, ..., a_n,a_n+1, ...}, or {a_n}.

The last form is given by a formula, as {n² + 1}

Remark that the (n+1)^th term a_n+1 ≠ a_n + 1. The integer (n + 1) is a subscript.

Not all the sequences have a general term. We can write down any sequence. For example:

{1, 4, 1, 4, 2, 1, 3, 5, 6, 2, 3, 7, ... }

An alternating sequences has alternated positive and negative terms. For example:

{- 2, + 4, - 8, + 16, ...}

Including the "..." means that the sequence is infinite.

2. Convergence of a sequence

2.1. Definitions

Let's consider a rod of length equal to 1. If one divides it in two parts (1/2, 1/2) and divides the second half in two parts (1/4,1/4), and so on, we get the following sequence when taking a half each time:

1/2, 1/4, 1/8, 1/16, ...

This sequence has the general term a_n = (1/2)ⁿ

If we continue dividing indefinitely each obtained half, we will find zero, that is a_n = 0. We say that the limit of the sequence {(1/2)ⁿ} is 0, and we can write:

lim an	= 0
n → ∞

For any sequence of general term a_n, when:

lim an = L   (L)

n → ∞

the sequence { an } is convergent.

If the limit L does not exist, or infinite, the sequence is divergent.

2.2. Alternating sequence

For an alternating sequence {(-1)ⁿb_n} with b_n > 0:

If lim bn	= 0 , the sequence is convergent to 0.
n → ∞

If lim bn	≠ 0 , the sequence is divergent.
n → ∞

2. Graphing a sequence

We can graph a sequence by plotting the points as n ranges over all possible values.

Example: The graph of the sequence {(2 n - 1)/n}:



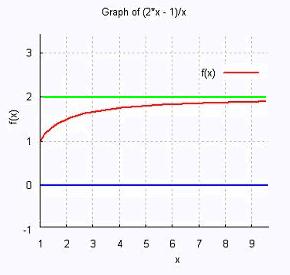
The graph shows the 11 first points of the 11 terms of the sequence.

We remark that as n increases, the terms in the sequence, get closer and closer to 2. We then say that 2 is the limit of the sequence and write:

lim an	= lim (2 n - 1)/n = 2
n → ∞	n → ∞