Calculus II
Contents
Series
Integrals
Definite integrals
Some primitives
Numerical methods
Exercices
© The scientific sentence. 2010
|
|
Calculus II:
Definite integral
numerical approaches
Trapezoidal rule
Trapezoidal rule is another numerical approach to evaluate
a definite integral.
In this method, we use trapezoids (or trapeziums). It gives a
better approximation to the area under the curve than
the rectangle method.
Trapezoidal rule
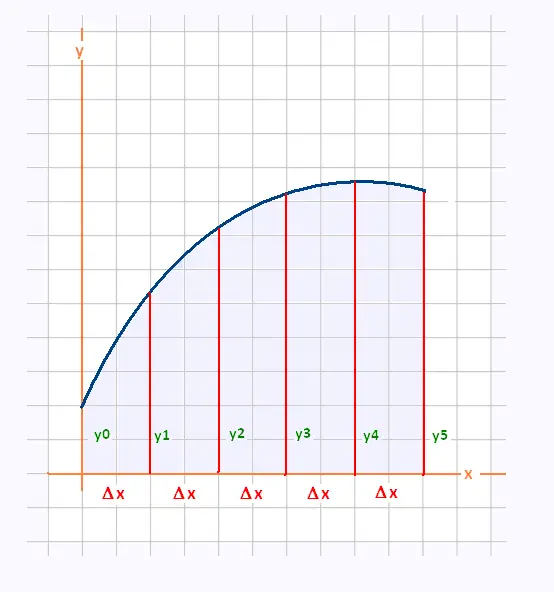
The area of a the first trapezoid is:
A1 = (y0 + y1)Δx/2
Δx is the « small change in x ».
The area of a the second trapezoid is:
A1 = (y1 + y2)Δx/2
An so on ...
So the approximate area under the curve is found by adding
the area of the trapezoids.
A = A1 + A1 + A2 + A3 + A4 + A5 =
(y0 + 2y1 + 2y2 + 2y3 + 2y4 + y5 )Δx/2
For n trapezoids we will have:
A =
(y0 + 2y1 + 2y2 + 2y3 + ... + 2yn-1 + yn )Δx/2
A =
Δx (y0/2 + y1 + y2 + y3 + ... + yn/2)
With
Δx = (b - a)/n
y0 = f(a)
yn = f(b)
yk = y0 + kΔx
Note that we get a better approximation if we take more
trapezoids . In this Δx will tend to 0.
Finally, if the curve of the function f is above the x-axis
between x = a and x = b
From a to b : Area = ∫ f(x) dx = Δx (y0/2 + y1 + y2 + y3 + ... +
yn/2)

|
|