Calculus II: Integration and trigonometric substitutions
Some integrands, mainly that contain radicals, are easily transformed into trigonometric expressions simple to integrate.
1. Trigonometric substitutions
The trigonometric identities:
cos2(x) = 1 - sin2(x)
sec2(x) = 1 + tan2(x)
tan2(x) = sec2(x) - 1
are used, by substituting cos(x), sec(x), or
tan(x), to eliminate radicals from integrals.
Sine-substitution x = a sin(θ) is used for an expression as
[a2 - x2]1/2
Tangent-substitution x = a tan(θ) is used for an expression as
[a2 + x2]1/2
Secant-substitution x = a sec(θ) is used for an expression as
[x2 - a2]1/2
2. Sine-substitution
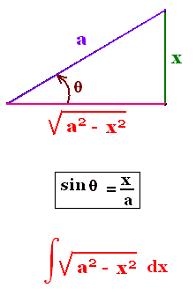
The integrand of the form :
f(x) = [a2 - x2]1/2,
is transformed into:
f(x) = a [1 - (x/a)2]1/2.
Then, we make the substitution
x/a = sin θ
So
dx = a cos θ dθ
Therefore
I = ∫ f(x) dx = ∫ [a2 - x2]1/2 dx =
a ∫[1 - (x/a)2]1/2 dx =
a2 ∫[1 - sin2 θ]1/2 cos θ dθ =
a2 ∫ cos2θ dθ =
Using the identity:
cos2z = (1 + cos (2z))/2
I = (a2/2) ∫ [1 + cos (2θ)] dθ =
(a2/2)[
∫ dθ + ∫ cos (2θ) dθ ] =
(a2/2)[
θ + (1/2) sin (2θ) ] =
∫ [a2 - x2]1/2 dx =
(a2/2)[ θ + (1/2) sin (2θ) ]
=
(a2/2)[
arcsin(x/a) + (1/2) sin (2θ)]
Since:
sin (2θ) = 2 sin (θ) cos(θ)
I = (a2/2)[
arcsin(x/a) + sin (θ) cos(θ)]
= (a2/2)[
arcsin(x/a) + (x/a)[1- (x/a)2]1/2 ]
Finally,
∫ [a2 - x2]1/2 dx =
(a2/2)[
arcsin(x/a) + (x/a)[1- (x/a)2]1/2] + cst.
∫ [a2 - x2]1/2 dx =
(a2/2)[
arcsin(x/a) + (x/a)[1 - (x/a)2]1/2 + cst.
3. Tangent-substitution
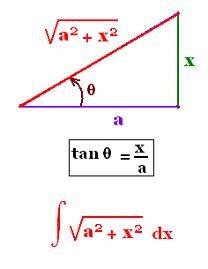
The the integrand of the form :
f(x) = [a2 + x2]1/2,
is transformed into:
f(x) = a [1 + (x/a)2]1/2.
Then, we make the substitution
x/a = tan θ
So
dx = a (1 + tan2θ) dθ = a sec2θ dθ
Therefore
I = ∫ f(x) dx = ∫ [a2 + x2]1/2 dx =
a ∫[1 + (x/a)2]1/2 dx =
a2 ∫[1 + tan2 θ]1/2 sec2θ dθ =
a2 ∫ sec3θ dθ =
a2 [(1/2) sec x tan x + (1/2) ln |sec x + tan x|] + const.
∫ [a2 + x2]1/2 dx =
a2 [(1/2) sec x tan x + (1/2) ln |sec x + tan x|] + const.
4. Secant-substitution
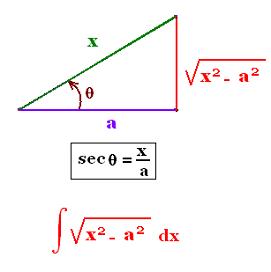
The the integrand of the form :
f(x) = [x2 - a2 ]1/2,
is transformed into:
f(x) = a [(x/a)2- 1]1/2.
Then, we make the substitution
x = a sec(θ)
So
dx = a sin θ sec2θ dθ
Therefore
S = ∫ f(x) dx = ∫ [x2 - a2]1/2 dx =
a ∫[(x/a)2 - 1]1/2 dx =
a2 ∫[sec2θ - 1]1/2 sin θ sec2θ dθ =
a2 ∫ tan θ sin θ sec2θ dθ =
a2 ∫ sin2 θ sec3θ dθ =
a2 ∫ [1 - cos2 θ] sec3θ dθ =
a2 [∫ sec3θ dθ
- ∫ cos2θ sec3θ dθ] =
a2 [∫ sec3θ dθ
- ∫ sec θ dθ] =
∫ sec3θ dθ =
(1/2) sec(θ). tan(θ) + (1/2)ln|(sec(θ) + tan(θ))| + cst
∫ sec θ dθ] = ln|(sec(θ) + tan(θ))| + cst
(These two integrals are calculated here.)
Therefore
S =
a2 [(1/2) sec(θ). tan(θ) + (1/2)ln|(sec(θ) + tan(θ))| + cst
- ln|(sec(θ) + tan(θ))| ] =
(a2 /2)[sec(θ). tan(θ) - ln|sec(θ) + tan(θ)|] + cst.
=
∫ [x2 - a2]1/2 dx =
(a2 /2)[sec(θ). tan(θ) - ln|sec(θ) + tan(θ)|] + cst.
5. Other forms with radical
5.1. Example 1
∫ [ax + b]1/n dx
Let
u = [ax + b]1/n, so
du = a (1/n) [ax + b]1/n - 1 dx
Therefore
∫ [ax + b]1/n dx =
∫ (n/a) u du [ax + b]1 - 1/n =
∫ (n/a) u du un/u =
∫ (n/a) du un =
[n/a(n + 1)] un + 1
Thus
∫ [ax + b]1/n dx =
[n/a(n + 1)] un + 1
∫(ax + b)1/n dx =
n un+1/a(n+1)
5.2. Example 2
∫ x2[1 - x]1/2 dx
Let u = [1 - x]1/2, so
u2 = 1 - x
Then
x = 1 - u2 , and dx = - 2 u du
Therefore
∫ x2[1 - x]1/2 dx =
∫ (1 - u2)2 u (- 2 u ) du =
- 2 ∫ (u2 - 2 u4 + u6) du
= - 2 [(1/3)u3 - (2/5)u5 + (1/7)u7 ] + cst.
= - 2 [(1/3)[1 - x]3/2 - (2/5)[1 - x]5/25 + (1/7)[1 - x]7/2 ] + cst.
∫ x2[1 - x]1/2 dx
= (- 2/3)(1 - x)3/2 + (4/5)(1 - x)5/2 -
(2/7)(1 - x)7/2 + cst.
5.3. Example 3
∫ x3[1 - x2]1/2 dx
Let u = [1 - x2]1/2, so
u2 = 1 - x2
Then
x2 = 1 - u2 , and 2 x dx = - 2 u du
or x dx = - u du
Therefore
∫ x3[1 - x2]1/2 dx =
∫ x2[1 - x2]1/2 x dx =
∫(1 - u2)u (- u) du =
- ∫(u2 - u4) du =
=
- [(1/3)u3 - (1/5)u5]
(1/5)u5 - (1/3)u3 =
(1/5)[1 - x2]5/2 - (1/3)[1 - x2]3/2 + cst.
∫ x3[1 - x2]1/2 dx
= (1/5)(1 - x2)5/2 - (1/3)(1 - x2)3/2 + cst.
|