Calculus III:
Double Integrals over general regions

1. The two regions

Consider a function z = f(x,y) of two variables x and y. We want to integrate this function over x and over z, not over a rectangle, but over a general region D :

∫∫_D f(x,y) dA

We have two possibilities:

1.1. Horizontal region

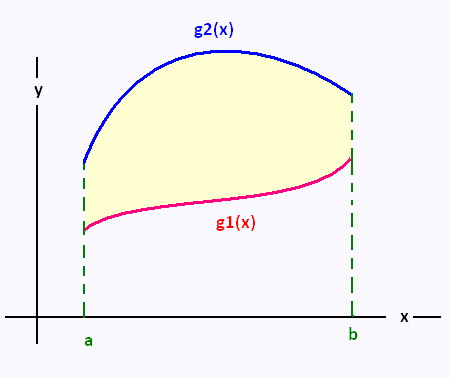
The integral is defined as:


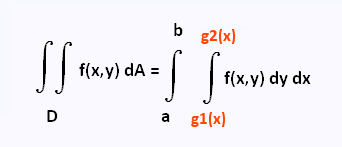
Where

D = {(x,y)| a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)}

1.2. Vertical region

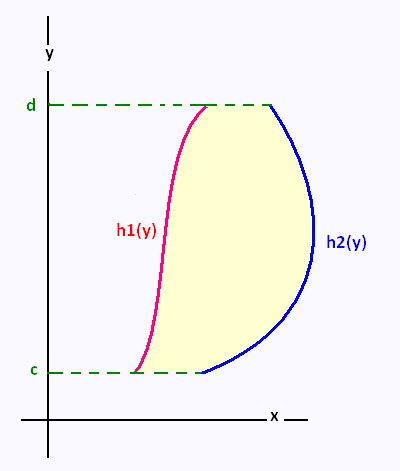
The integral is defined as:



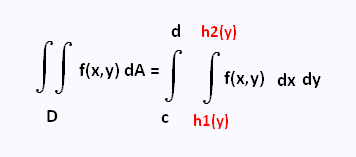
Where D = {(x,y)| h1(y) ≤ x ≤ h2(y), c ≤ y ≤ d}

The essential task in these kind of problems is to determine the region over we integrate.

2. Exemples

Exemple 1

∫∫_D 2xy - y² dA

Where D is the region bounded by y = √x and y = x²



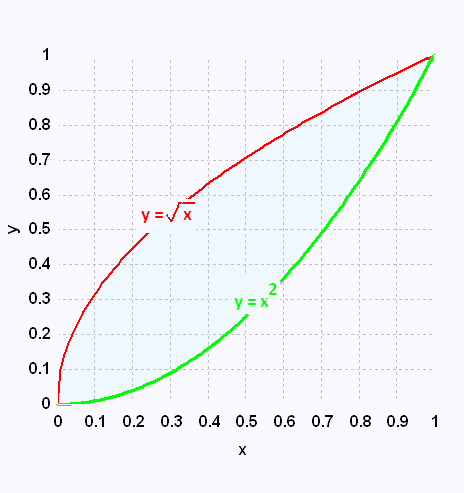
∫∫D f(x,y) dA = ∫ 01 ∫x2√x 2xy - y2 dy dx

= ∫ 01 xy2 - y3/3 | x2√x dx = ∫ 01 x2 - x3/2/3 - x5 + x6/3 dx
= x3/3 - (2/15) x5/2 - x6/6 + x7/21 |01 = - 1/6 + 1/21 + 1/3 - 2/15 = 17/210

∫∫_D 2xy - y² dA = 17/210

Remark:

If we have used the vertical region form, we will find the same result:

∫∫D f(x,y) dA = ∫01 ∫y2√y f(x,y) dx dy

Exemple 2

∫∫_D f(x,y) dA

Where D is the triangle with vertices
(1,4), (2,1), and (6,3)



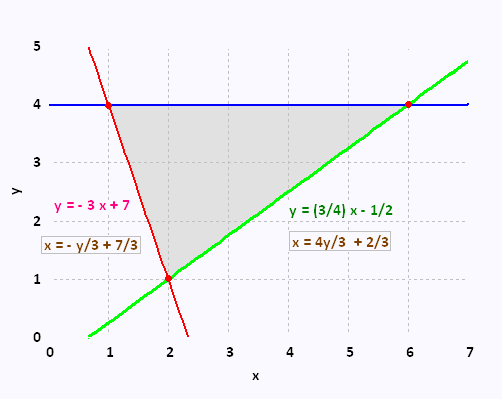
• First method: We use the vertical region form:

∫∫_D f(x,y) dA = ∫₁⁴ ∫_{- y/3 + 7/3} ^{4y/3 + 2/3} f(x,y) dx dy

• Second method:

We can also break the region up into two different pieces and write the region D as the union of two other regions D1 and D2.

D = D1 ∪ D2 where

D1 = {(x,y) | 0 ≤ x ≤ 1, -2x+3 ≤ y ≤ 3}

D2 = {(x,y) | 1 ≤ x ≤ 5, x/2 + 1/2 ≤ y ≤ 3}

So

∫∫_D f(x,y) dA = ∫₀¹ ∫_-2x+3³f(x,y) dy dx + ∫₁⁵ ∫_{x/2 + 1/2}³f(x,y) dy dx

Exemple 3

∫∫_D f(x,y) dA

Where D is the region delimited by the line y = 4 and the parabola of equation y = x²/4.

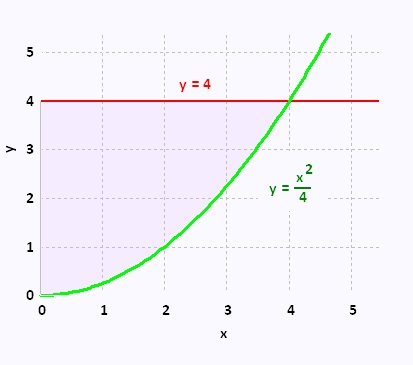
• First method: We use the vertical region form:

∫∫_D f(x,y) dA = ∫₀⁴ ∫₀ ^√2y f(x,y) dx dy

• Second method: We use the horizontal region form:

∫∫_D f(x,y) dA = ∫₀⁴ ∫_x²/4⁴ f(x,y) dy dx