Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III: The 3-D Coordinate System
1. Geometry of the 3D Coordinate System
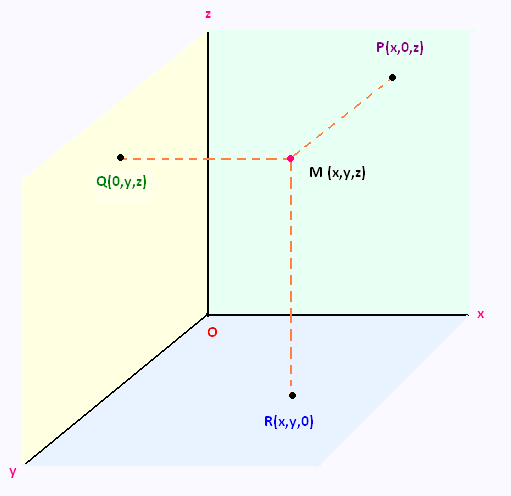
The 1D coordinate system is denoted by R . The 2D coordinate system is
denoted by R2.
The 3D coordinate system (O,x,y,z) is denoted by R3,
and the n dimensional coordinate system is often denoted by Rn .
In the figure, the point M is the point in the 3D space. Starting at M and
moving down, the point R sits in the xy-plane. The xy-plane corresponds
to all the points in space which have a zero z-coordinate.
Also start at M and move in the other two directions as shown, we
get the points P and Q in the xz-plane and the yz-plane. The xz-plane
is the plane where all the points have a zero y-coordinate, and
the yz-plane is the plane where all the points have a zero x-coordinate.
The xy, xz, and yz-planes are the coordinate planes. The point R, P, and Q
are the projection of the point M in the xy-plane, xz-plane, and
yz-plane respectively.
2. From 2D to 3D Coordinate Systems
Some of the formulas used in R2 space are extended in
R3.
For instance:
• The Pythagoras theorem:
OM = √(OR2 + OP2 + OQ2)
• The distance between two points M1(x1,y1,z1) and
M2(x2,y2,z2) is :
D(M1,M2) = √[(x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2]
• The equation for a sphere with center C(a,b,c)
and radius r is :
(x - a)2 + (y - b)2 + (z - c)2 = r2
• The similarity ratio k in 1D system is k2 in R2 ,
and k3 in R3.
|
|