Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Equation of a plane in 3D space
1. Equation of a plane in 3D space
1.1. The vector equation of the plane
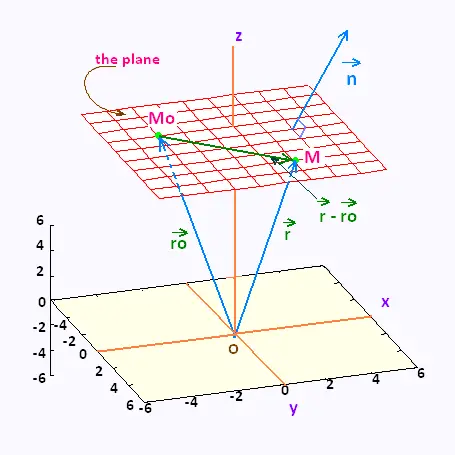
Let�s suppose that we know a point Mo(xo,yo,zo) that is on the plane.
Let's consider any point M(x,y,z) on the plane is any point in the plane.
The plane has a normal vector 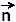 (a,b,c) that is orthogonal to this plane. It has not to touch the plane, just
perpendiculat to it. (a,b,c) that is orthogonal to this plane. It has not to touch the plane, just
perpendiculat to it.
 , and , and are the position vectors for Mo and M respectively. are the position vectors for Mo and M respectively.
The resultant vector  - - lies in the plane.
lies in the plane.
The normal vector 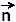 is orthogonal to the plane.
It is also orthogonal to any vector that lies in the plane. In particular it is s orthogonal to is orthogonal to the plane.
It is also orthogonal to any vector that lies in the plane. In particular it is s orthogonal to  - - . .
Using the property of the Dot Product :« two orthogonal vectors have a dot product of zero ». That is is:
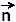 • ( • ( - - ) = 0 ) = 0
That can be written as:
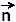 • • = =
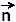 • •
This is the vector equation of the plane.
1.2. The scalar equation of the plane
Using the definition of the dot product, in the cartesian coordinates
system, we can write:
(a, b, c) . (x - xo, y - yo, z - zo) = 0
We obtain:
a (x - xo) + b (y - yo) + c (z - zo) = 0
Developing and rearranging, and setting
d = a xo + b yo + c zo yield:
a x + b y + c z = d
Gnerally , with - d = D, this equation is written as follows:
A x + B y + C z + D = 0
All these forms are called the scalar equation of a plane .
2. Exercices
2.1. Exercice 1
Determine the equation of the plane that contains the following three
points P(1,-4,1), Q(- 2,3, 2), and R(2, - 1, 3) .
Solution:
From these three points we build two vectors, then the normal vector of the plane using the cross product, and we use one of them as the known
point.
These three points are located on the plane. From them,
we build two vectors that lies in the plane:
PQ = (-3 , 7, 1)
PR = (1, 3, 2)
The cross product of the two vectors is orthogonal
to both of these vectors, then to the plane.
(-3 , 7, 1) x (1, 3, 2) =
= (11, 7, - 16). So
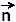 = (11, 7, - 16) = (11, 7, - 16)
Using R as the known point ( we could have used any of the three points),
we obtain:
d = 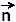 • • = (11, 7, - 16) . (1, 3, 2) = 11 + 21 - 32 = 0 = (11, 7, - 16) . (1, 3, 2) = 11 + 21 - 32 = 0
D = - d = 0
The scalar equation of the plane is:
11 x + 7 y - 16 z = 0
2.2. Exercice 2
A plane is given by a scalar equation :
2 x - 3 y + 4 = 6
, and
a line is given by the vector form:
 = (2 - t, 1 + 2 t, - 3)
. = (2 - t, 1 + 2 t, - 3)
.
We ask to determine whether the plane and the line are orthogonal,
parallel or neither.
Solution:
The normal vector for the plane is
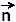 = (2, - 3, 4) = (2, - 3, 4)
The parallel vector for the line is
 = (- 1, 2, 0) = (- 1, 2, 0)
How are the two vectors 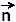 , and , and  ? ?
a) Are there parallel ?
In this case, is their cross product equal to zero?
(2, - 3, 4) x (- 1, 2, 0) =
= ( - 8, - 4, 1) ≠ 0 .
So the two vectors are not parallel, hence
the plane and the line are not orthogonal.
c) Are there orthogonal ?
In this case, is their dot product equal to zero?
(2, - 3, 4) • (- 1, 2, 0)
= - 2 - 6 + 0 = - 8 ≠ 0 .
So the two vectors are not orthogonal,
hence the plane and the line are not parallel.
Conclusion:
The plane and the line are neither parallel nor orthogonal.
|
|