Calculus III:

Functions of two variables
Absolute Minimums and Maximums

We are going to determine the absolute extrema and critical points of a fonction of two variables.

1. Extreme Value Theorem

To optimize a function f(x,y) in a given region D of the xy-plane in 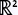, we identify the absolute minimum and/or the absolute maximum of this function, on the region D .

Definitions:

1. A region in 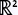, that is in the xy-plane, is called closed if it includes its boundary. A region is called open if it doesn’t include any of its boundary points.

2. A region in 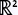is called bounded if it is defined delimited. In other words, a region is bounded if it is finite.

Extreme Value Theorem :

If f(x,y) is continuous in some closed, bounded set D in 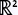then there are points in D, (x1,y1) and (x2, y2) so that (x1,y1) is the absolute maximum and (x2,y2)is the absolute minimum of the function in D.

An absolute minimum and/or absolute maximum may occur in the interior of the region or it may occur on the boundary of the region.

2. Finding Absolute Extrema

The method consists of tn three steps:

1.Find all the critical points of the function that lie inside the region D and determine the function value at each of these points.

2. Find all extrema of the function on the boundary.

3. The largest and smallest values found in the first two steps are the absolute minimum and the absolute maximum of the function.

3. Summary
Absolute Maximum and Minimum Values

If f is a continuous function of two variables x and y on a closed and bounded region D in ,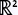
then f attains an absolute maximum value and an absolute minimum value at some points in D.

To find the absolute maximum and minimum values of f on D:

(1) Find the values of f at the critical points of f in the interior of D.
(2) Find the extreme values of f on the boundary of D.
(3) The largest of the values from steps 1 and 2 is the absolute maximum value; the smallest of these values is the absolute minimum value.

Example

Find the absolute maximum and minimum values of the function

f(x, y) = - x² - y² + 2x + 2y + 1
on the triangular region in the first quadrant bounded by the lines x = 0, y = 0, and y = 2 - x.

1. Inside D:

f_x = - 2 x + 2 = 0 ⇒ x = 1
f_y = - 2 y + 2 = 0 ⇒ y = 1
So f(1,1) = 3 .
We have then one CP (1,1). So f(1,1) = 3 .

2. In the boundary of D:

At three vertices we have

f(0, 0) = 1,
f(2, 0) = 1,
f(0, 2) = 1.

On the three edges

• On the line segment y = 0, 0 ≤ x ≤ 2,

we have g1(x) = f(x,0) = - x² + 2x + 1. Hence, g1'(x) = - 2x + 2 and
g1'(x) = 0 yields x = 1 . So f(1,0) = 2.

• On the line segment x = 0, 0 ≤ y ≤ 2,

we have g2(y) = f(0,y) = - y² + 2y + 1. Hence, g2'(y) = - 2y + 2 and
g2'(y) = 0 yields y = 1 . So f(0,1) = 2.

• On the line segment 0 ≤ x ≤ 2, y = 2 - x

we have g3(x) = f(x,2 - x) = - x² - (2 - x)² + 2x + 2(2 - x) + 1 = - 2 x² + 4 x + 1.

Hence, g3'(x) = - 4x + 4 and g3'(x) = 0 yields x = 1 .
So y = 2 - 1 = 1 . f(1,1) = 3.

Here is then the set of all the critical points:

{f(1,1) = 3, f(0, 0) = 1, f(2, 0) = 1, f(0, 2) = 1, f(1,0) = 2, f(0,1) = 2, }

Conclusion:

The function f achieves the maximum value 3 at (1, 1) and the minimum value 1 at the points (0, 0), (2, 0), and (0, 2).