Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector functions
Arc Length of a vector function
1. Arc Length of a vector function
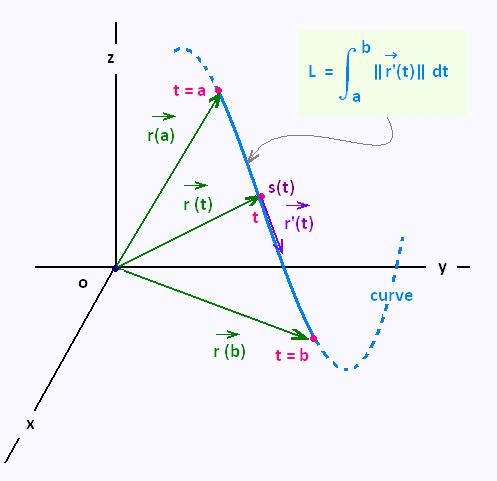
Let consider the vector function  (t) = 〈 f(t), g(t), h(t) 〉 (t) = 〈 f(t), g(t), h(t) 〉
We want to determine le length of the curve related to this vector function
on the interval a ≤ t ≤ b.
If we write this vector function into the parametric form, we
will have:
x = f(t) , y = g(t), z = h(t), and the arc length is given by
L = ∫ab √{f'(t)2 + g'(t)2 + h'(t)2} dt.
The integrand is the magnitude of the tangent vector, so:
L = ∫ab|| (t)|| dt (t)|| dt
Example
Let's consider the following vector function:
 (t) = (2t, - cos t, sin t) (t) = (2t, - cos t, sin t)
We want to determine le length of the curve  on the interval 0≤ t ≤ 4.
on the interval 0≤ t ≤ 4.
So  (t) = 〈 2, sin t, cos t 〉 (t) = 〈 2, sin t, cos t 〉
The length of this tangent vector is:
|| (t)|| = sqrt(22 + sin2t
+ cos2t) = √5 (t)|| = sqrt(22 + sin2t
+ cos2t) = √5
The length is then:
L = ∫04√5 dt = 4 √5.
2. Arc length function s(t)
We want to know the length of the arc s(t) at a certain time t, and the
express the vector function  (t) in termes of s. (t) in termes of s.
This allow to determine the final point on the curve after traveling
a distance s.
The length of the arc s(t) can be written as:
s(t) = ∫0t || (ξ)|| dξ, (ξ)|| dξ,
where ξ is a spacial variable along the curve.
Example
Let's determine the arc length function for
 (t) =
〈 2t, - cos t, sin t 〉 . (t) =
〈 2t, - cos t, sin t 〉 .
After travelling a distance of 2π√5, where is then the
final point on the curve ?
 (t) = 〈 2t, - cos t, sin t 〉. So (t) = 〈 2t, - cos t, sin t 〉. So
 (t) = 〈 2, sin t, cos t 〉 (t) = 〈 2, sin t, cos t 〉
|| (t)|| = sqrt(22 + sin2t
+ cos2t) = √5 (t)|| = sqrt(22 + sin2t
+ cos2t) = √5
Therefore
s(t) = ∫0t || (ξ)|| dξ
= ∫0t √5 dξ = √5 t (ξ)|| dξ
= ∫0t √5 dξ = √5 t
s(t) = √5 t → t = s/√5
In terms, of s, the original vector function becomes:
 (t) = 〈 2s/√5, - cos (s/√5), sin (s/√5) 〉. (t) = 〈 2s/√5, - cos (s/√5), sin (s/√5) 〉.
With the reparameterization we can now tell where we are on the curve after we�ve traveled a distance of s = 2π√5 = 14.04 units, along the curve. We start the measurement of distance from t = 0.
 (s) = 〈 2s/√5, - cos (s/√5), sin (s/√5) 〉. (s) = 〈 2s/√5, - cos (s/√5), sin (s/√5) 〉.
 (s = 2π√5) = 〈 4π, - 1, 0 〉. (s = 2π√5) = 〈 4π, - 1, 0 〉.
So, after raveling a distance of s = 2π√5 = 14.04 units
on the curve, we are at the point:
 (s = 2π√5) = 〈 4π, - 1, 0 〉 (s = 2π√5) = 〈 4π, - 1, 0 〉
|
|