Calculus III:

Conservative vector fields

Let's recall that if a vector field is conservative then ∫_C. 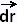is independent of path.

This comes from that if the vector field is conservative then it is associated to a potential function f such as ∇f = , and, in turn, using the fondamental theorem of line integrals.

Now, given a vector field , we want to:

• determine whether is conservative, and
• If so, determine its potential function f.

1. Given . Is it conservative ?

Given a vector field, we want to identify if it is conservative.

The vector field is conservative. It is then associated to a potential function f such as ∇f =

= P + Q = (∂f/∂x) + (∂f/∂y). So

∂f/∂x = P
∂f/∂y = Q

Taking the partial derivative, we obtain:

∂²f/∂x∂y = ∂P/∂y
∂²f/∂y∂x = ∂Q/∂x

Therefore

∂P/∂y = ∂Q/∂x

Theorem:

Let = P + Q be a vector field on an open and simply-connected region D.
If P and Q have continuous first order partial derivatives in D and ∂P/∂y = ∂Q/∂x,
then the vector field is conservative.

Example 1

Determine if the vector fields
(x,y) = (x² + y) + (y² + x)
is conservative or not.

We have:

P(x,y) = x² + y
Q(x,y) = y² + x

∂P/∂y = 1
∂Q/∂x = 1

∂P/∂y = ∂Q/∂x

(x,y) is conservative.

Example 2

Determine if the vector fields
(x,y) = (x² + xy) + (y² + xy)
is conservative or not.

We have:

P(x,y) = x² + xy
Q(x,y) = y² + xy

∂P/∂y = x
∂Q/∂x = y

∂P/∂y ≠ ∂Q/∂x

(x,y) is not conservative.

2. is conservative.
What is its potential function Æ’ ?

Given a conservative vector field, we want to determine the potential function Æ’ for this vector field.

Let’s assume that the vector field is conservative and so we know that a potential function, f(x,y) exists. We can then write:

∇f = (∂f/∂x) + (∂f/∂y) = P + Q = .

That is, by setting the two components equal:

∂f/∂x = P, and
∂f/∂y = Q

By integrating each of these, we obtain the two following equations.

f(x,y) = ∫P(x,y) dx    or    f(x,y) = ∫Q(x,y) dy

Example 3

Determine if the vector field
= (x²y³ + x) + (x³y² + y)
is conservative and if so, find a potential function for this vector field.

We have:

P(x,y) = x²y³ + x
Q(x,y) = x³y² + y

∂P/∂y = 3 x²y²
∂Q/∂x = 3 x²y²

∂P/∂y = ∂Q/∂x

So (x,y) is conservative.

Now let’s find the potential function:

f(x,y) = ∫P(x,y) dx = ∫ (x²y³ + x) dx =
(1/3)x³y³ + (1/2) x² + c(y)

c(y) is the a function of y.
This function is constant with respect to x.

f(x,y) = ∫Q(x,y) dy = ∫ (x³y² + y) dy =
(1/3)x³y³ + (1/2) y² + c(x)

c(x) is a function of x.
This function is constant with respect to y.

Let's work on the first integral:

f(x,y) = (1/3)x³y³ + (1/2) x² + c(y)

We now need to determine c(y) .

Let’s differentiate f(x,y) with respect to y and set it equal to Q:

∂f/∂y = x³y² + ∂c(y)/∂y = Q = x³y² + y.

Hence ∂c(y)/∂y = y , and then

c(y) = (1/2) y² + const.

Threrfore

f(x,y) = (1/3)x³y³ + (1/2) x² + (1/2) y² + const.

The constant const can be anything. So there are an infinite number of possible potential functions, although they will differ by an additive constant.

3. Three-dimentional conservative vector fields

In three-dimentional space, for a conservative vector field (x,y,z) having f as a potential function, we can write:

∇f = (∂f/∂x) + (∂f/∂y) + (∂f/∂z) =
P + Q + R = .

Example 4

Find the potential function for the vector field
(x,y,z) = 2xy²z³ + 2x²yz³ + 3x²y²z²


We will see in the second next section that the curl of this vector field (x,y,z) in zero. So this vector field is conservative.

Now, we have:

P(x,y,z) = ∂f/∂x = 2xy²z³
Q(x,y,z) = ∂f/∂y = 2x²yz³
R(x,y,z) = ∂f/∂z = 3x²y²z²

Let’s find the potential function:

Let's integrate the first one with respect to x :

f(x,y,z) = x²y²z³ + c(y,z)

• Now, we differentiate this with respect to y and set it equal to Q:

2x²yz³ + ∂c(y,z)/∂y = 2x²yz³

Hence ∂c(y,z)/∂y = 0. That is c(y,z) = c(z)

Therefore

f(x,y,z) = x²y²z³ + c(z)

• Now, we differentiate with respect to z and set the result equal to R:

3x²y²z² + ∂c(z)/∂z = 3x²y²z²

Hence ∂c(z)/∂z = 0. That is c(z) = const.

The potential function for this vector field is then:

f(x,y,z) = x²y²z³ + const.