Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Functions of two variables
Relative extrema of a function of two variables
Critical points of a function of two variables
We are going to determine the relative extrema and critical points of a fonction of two variables.
1. Relative extrema
The definition of relative extrema , that refer to both minimums and maximums, for functions of two variables is identical to that for functions of one variable.
Here is the definition of relative minimum and relative maximum for functions of two variables.
• A function f(x,y) has a relative minimum at the point (a,b) if
f(x,y) ≥ f(a,b) for all points (x,y) in some region around (a,b) .
• A function f(x,y) has a relative maximum at the point (a,b) if
f(x,y) ≤ f(a,b) for all points (x,y)
in some region around (a,b).
Note the term some region around the point. That means the relative minimum is not the smallest, and the relative maximum is not the largest, values that the function will ever take. The relative extrema are not alone for a function.
Outside of that region it is completely possible for the function to be smaller or larger.
2. Critical points
We extend the definition of the critical point, called also stationary point, from functions of one variable to functions of two variables.
The critical point of the function y = f(x)
is a number x = c so that either f'(c) = 0 or
f'(c) doesn�t exist.
We have a similar definition for critical points of functions of two variables.
The point (a,b) is a critical point of f(x,y) if :
• ∇f(a,b) = 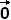 , that is
fx = 0 AND fy = 0, or , that is
fx = 0 AND fy = 0, or
• fx(a,b) and/or fy(a,b) doesn�t exist.
3. A relative extrema is also a critical point
We want to make sur that if the point (a,b) is a relative
extrema of the function f(x,y), then (a,b)
is also a critical point of f(x,y).
In other words,
If the point (a,b) is a relative extrema of the function f(x,y),
then ∇f = 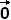 . .
Here is sthe proof:
Let's suppose that f(x,y) has a relative extrema at (a,b). Let�s define a
function with one variable g(x) = f(x,b). This function has then a relative extrema at x = a
as f(x,y). So g'(a) = fx(a,b) = 0
The same process for a function h(y) = f(a,y) leads to fy(a,b) = 0
Therefore
fx(a,b) + fy(a,b) = 0. That is
∇f = 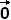 , and so f(x,y) has a critical point at
(a,b). , and so f(x,y) has a critical point at
(a,b).
A relative extrema of a function f(x,y)
is also a critical point of f(x,y).
4. A critical point is not necessarily a
relative extrema :
saddle point
We said : a relative extrema of a function f(x,y)
is a critical point of f(x,y).
Now, the reciprocal is not true. Not all the critical points
are the extrema for a function.
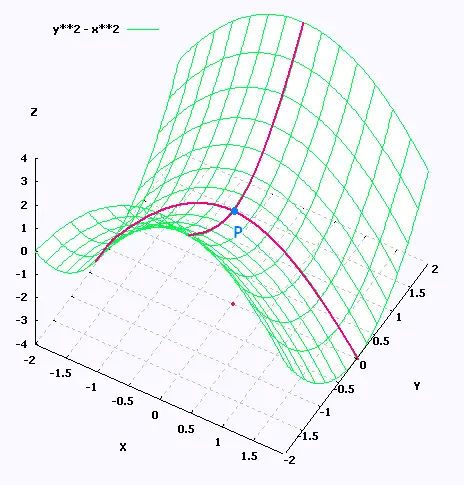
Among the critical points
that are not extrema for a function are the saddle points.
Here is an example for the function f(x,y) = x2 - y2:
We have fx = 2x , and fy = - 2y
The only point that will make both of these derivatives zero
at the same time is (0,0). So (0,0) is a critical point for
the function.
But at the point (0,0) f(x,y) presents a maximum along the x-axis, and
a minimum along tyhe y-axis. Hence the point (0,0) is nit an extrma.
Therefore this saddle point (0,0) is a critical point, but
not an extrema.
So all relative extrema are critical points, but it is possible that at
least one of the critical points won�t be a relative extrema.
Once all the critical points in hand, what to to see if they are relative extrema or not?
To determine if a critical point is a relative extrema, that is a minimum or a maximum,
we use the following test:
Suppose that (a,b) is a critical point of f(x,y) and that the second
order partial derivatives are continuous in some region that contains
(a,b).
We definine the following criterium:
D = D(a,b) = fxx(a,b) fyy(a,b) - [fxy]2
We then have the following classifications of the critical point.
• If D > 0 and fxx(a,b) > 0, then (a,b) is a relative minimum .
• If D > 0 and fxx(a,b) < 0, then (a,b) is a relative maximum .
• If D < 0, then the point (a,b) is a saddle point.
• If D = 0, then the point may be a relative minimum, relative maximum or a saddle point.
Other techniques would be used to classify this critical point.
Example 1
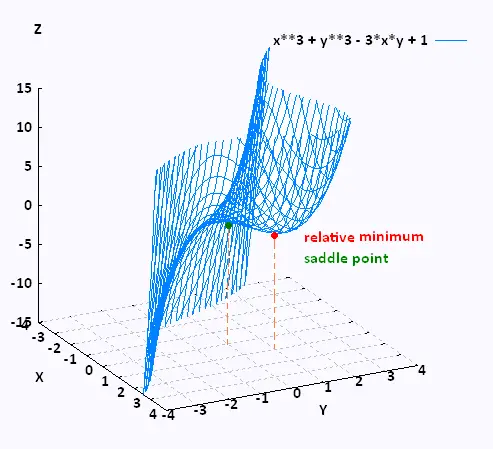
Find and classify all the critical points of f(x,y) = x3 + y3 - 3xy + 1.
C.P. ∇f = 
fx = 0 : 3x2y - 3y = 0 ⇒ y = x2
fy = 0 : 3y2 - 3x = 0 ⇒ y2 = x
⇒ x4 = x
⇒ x(x3 - 1) = 0 ⇒ x = {0,1}
C.P. (x,y) = {(0,0),(1,1)}
Classification:
D = fxx . fyy - (fxy)2 =
(6x)(6y) - (- 3)2 = 36 xy - 9
D(0,0) = - 9 < 0 ⇒ saddle point at (0,0)
D(1,1) = 36 - 9 > 0 , fxx(1,1) = 6 > 0 ⇒ relative minimum at (1,1).
Example 2
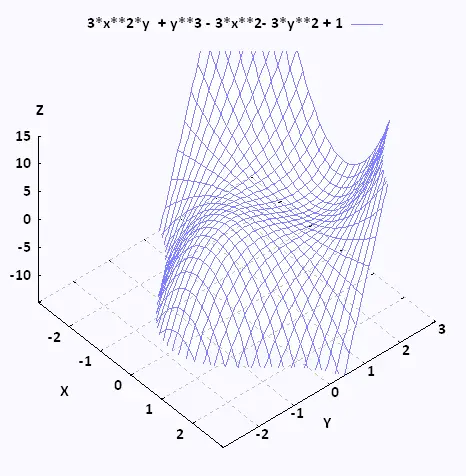
Find and classify all the critical points of f(x,y) = 3x2y + y3 - 3x2 - 3y2 + 1.
C.P. ∇f = 
fx = 0 : 6 xy - 6x = 0 ⇒ 6x(y - 1) = 0 ⇒ x = 0, y = 1
fy = 0 : 3x2 + 3y2 - 6y = 0
x = 0 : 3y2 - 6y = 0 ⇒ y2 - 2y = 0 ⇒ y(y - 2) = 0
⇒ y = {0,2}
(x,y) = {(0,0), (0,2)}
y = 1 : 3x2 + 3 - 6 = 0 ⇒ 3x2 - 3 = 0 ⇒ x2 - 1 = 0
⇒x = ± 1 ⇒ y = {(- 1,1), (1, 1)}
We get a total of C.P.'s:
(x,y) = {(0,0), (0,2), (- 1,1), (1, 1) }
Classification:
D = fxx . fyy - (fxy)2 =
(6y - 6)(6y - 6) - (6x)2 = (6y - 6)2 - (6x)2 =
36[(y - 1)2 - x2)
D(0,0) = 36 < 0, fxx(0,0) = - 6 < 0 ⇒ relative maximum at (0,0)
D(0,2) = 36 > 0 , fxx(0,2) = 6 < 0 ⇒ relative minimum at (0.2).
D(- 1, 1) = - 36 < 0 , fxx(0,2) = 6 < 0 ⇒ saddle point at (- 1,1).
D(1,1) = - 36 < 0 , fxx(0,2) = 6 < 0 ⇒ saddle point at (1,1).
|
|