Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III
Vector operators
Applications
Curl and divergence of a vector
In Physics,  being the velocity vector field of
a moving object, this object is irrotational when curl ( being the velocity vector field of
a moving object, this object is irrotational when curl ( ) = ) = 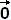 and incompressible when div ( and incompressible when div ( ) = 0. ) = 0.
1. Curl of a vector
Given the vector field  =
P =
P  +
Q +
Q  +
R +
R  ,
the curl of the vector ,
the curl of the vector  is defined by
the cross product: is defined by
the cross product:
Curl ( ) = ∇ × ) = ∇ × 
∇ = ∂ is the partial differential operator.
That is the gradient vector, that acts on a scalar as a function, to give a vector.
∇ = ∂ =
(∂/∂x) +
(∂/∂y) +
(∂/∂y) +
(∂/∂z) +
(∂/∂z)
Acting on a function f, yields:
∇f
= (∂f/∂x)  +
(∂f/∂y) +
(∂f/∂y)  +
((∂f/∂z) +
((∂f/∂z) 
Therefore
The
curl of a vector is the cross product of the gradient vector ∇ and
the vector itself.
= (Ry - Qx)  +
(Pz - Rx) +
(Pz - Rx)  +
(Qx - Py) +
(Qx - Py) 
2. Properties of the curl operator
• If f(x,y,z) has continuous second order partial derivatives then
curl(∇f) = 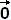 . .
• If  is a conservative vector field then
curl( is a conservative vector field then
curl( ) = ) = 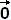 . That is the
definition of a conservative vector field. . That is the
definition of a conservative vector field.
• If  is defined on is defined on 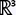 ,
has its components continuous first order partial derivative, and
curl ( ,
has its components continuous first order partial derivative, and
curl ( ) = ) = 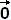 , then , then
 is a conservative vector field. is a conservative vector field.
3. Divergence operator
Given the vector field  =
P =
P  +
Q +
Q  +
R +
R  ,
the divergence of the vector ,
the divergence of the vector  is defined by
the dot product: is defined by
the dot product:
div ( ) = ∇ . ) = ∇ . 
∇ = ∂ is the partial differential operator.
That is the gradient vector, that acts on a vector to give a scalar.
∇ = ∂ =
(∂/∂x) +
(∂/∂y) +
(∂/∂y) +
(∂/∂z) +
(∂/∂z)
Acting on a vector  , yields: , yields:
∇ .  ,
= ∂P/∂x +
∂Q/∂y +
∂R/∂z ,
= ∂P/∂x +
∂Q/∂y +
∂R/∂z
Therefore
The divergence of a vector is the dot product of the gradient vector ∇ and
the vector itself.
4. Property of divergence-curl operator
• Relationship between the curl and the divergence:
div (curl  ) = 0 ) = 0
|
|