Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector functions
Curvature
Curvature
We will determine, in this section, the curvature of a smooth curve
or helix ,
that is a curve with  (t) continuous for all t's,
and (t) continuous for all t's,
and  (t) ≠ (t) ≠ 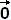 (s). (s).
At a given point, the curvature measures how fast a curve is changing direction
.
The formal definition of curvature is:
κ = |d (t)/ds| (t)/ds|
Where
 is the unit tangent and s is the arc length. is the unit tangent and s is the arc length.
We can also use the following formulas:
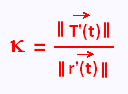
or
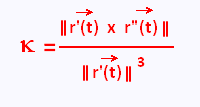
In the case of a function of one variable, y = f(x), we have
 (t) = x (t) = x + f(x) + f(x) , and the curvature is , and the curvature is
κ = |f'(x)|/[1 + (f'(x))2]3/2
Example
Let's determine the curvature for the vector function:
 (t) = (1, t, 2t) (t) = (1, t, 2t)
 (t) = 〈 0, 1, 2 〉 (t) = 〈 0, 1, 2 〉
|| (t)|| = √5 (t)|| = √5
 (t) = 〈 0, 1, 2 〉 /√5 (t) = 〈 0, 1, 2 〉 /√5
 '(t) = 〈 0, 0, 0 〉 /√5 = '(t) = 〈 0, 0, 0 〉 /√5 =
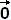
||  '(t)|| = 0 '(t)|| = 0
The curvature κ = 0/√5 = 0
|
|