Calculus III: parametric equations
Cycloid
1. Parametric equations for the cycloid
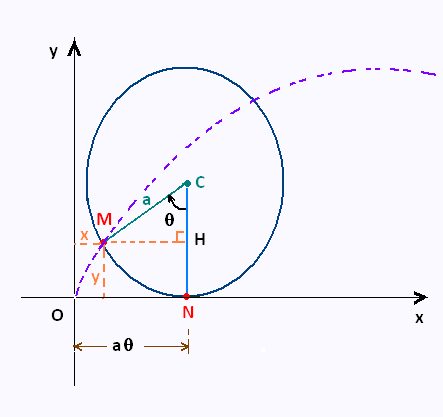
A cycloid is the curve traced by a point on a circle as it rolls along a straight line.
NM = ON
A moving point on the circle goes from O(0,0) to M(x,y). It describes the arc NM of length
equal to a θ .
The coordinates x and y of the point M are:
x = ON - MH = aθ - a sin θ
y = CN - CH = a - a cos θ
so the parametric equations for the cycloid are:
x = a (θ - sin θ)
y = a(1 - cos θ)
1.1. Area under an arch of a cycloid
The the parametric equations of the cycloid , we get the
corresponding derivatives :
dx = a (dθ - cos θ dθ)
dy = a sin θ dθ
with 0 ≤ θ ≤ 2π
The area under the arch is:
∫02π y dx =
∫02π a(1 - cos θ) a (dθ - cos θ dθ) =
a2 ∫02π (1 - cos θ)2 dθ =
a2 ∫02π ((3/2)θ - 2 sin θ + (1/2) sin θ cos θ) dθ = 3 π a2
so the area under an arch is:
A = 3 π a2
1.2. Arch length of the cycloid
S = ∫02π [(dx/dθ)2 + (dy/dθ)2]1/2 dθ =
= ∫02π a[2 - 2 cos θ]1/2 dθ =
= ∫02π 2a |sin(θ/2)| dθ =
= 2∫0π 2a sin(θ/2) dθ = 8 a
so the arc length of one arch of a cycloid is:
S = 8 a
2. The inverted cycloid
Rotated through 180o, we get the inverted cycloid,
an intersting curbe in Physics.
The inverted cycloid is the curve of fastest descent under gravity.
We can prove this by using the Lagrangian formalism.
|