Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Partial derivatives
Directional derivatives
1. The unit vector directional
of the change of a function
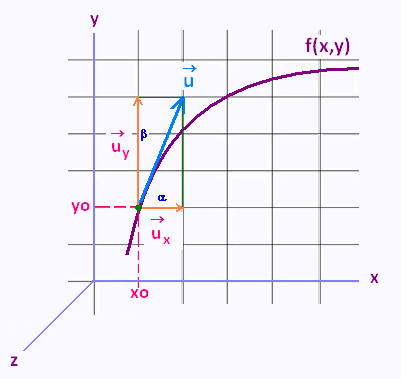
Directional derivatives are derivatives along a
unit vector.
The two partial derivatives fx and fy represent respectively the rate of change of f as we vary x and holding y fixed; and as we vary y and holding x fixed .
Now, we need to know what is the rate of change of the function f if we change both x and y simultaneously.
So, let's suppose that we want te define the rate of change of f at a particular point, say (xo, yo).
Let�s also suppose that x changes by α and y changes by β; that is
xo becomes x = x0 + αh and
yo becomes y = yo + βh.
The parameter h is the measure of the change.
For example if the unit vector
 = 〈1/√10, 3√10〉, the point
(xo, yo) becomes the point (xo + h/√10, yo + 3h/√10). = 〈1/√10, 3√10〉, the point
(xo, yo) becomes the point (xo + h/√10, yo + 3h/√10).
α and β are the coordinates of the unit
vector  at the point (xo,yo).
They are the units of measure of the change along x-axis
and y-axis. at the point (xo,yo).
They are the units of measure of the change along x-axis
and y-axis.
The direction of the vector  is the direction of the variation of change. is the direction of the variation of change.
Note that if we want the direction of change as
an angle θ say θ = π/4, we express the unit vector  in termes of this angle, that is in termes of this angle, that is
 = 〈cos θ, sin θ 〉 = 〈cos θ, sin θ 〉
2. Definitions
The derivative of a function of a single variable is the rate of change defined by :
Df(x) = lim (f(x + h) - f(x))/h
h → 0
That can be written as a directional derivative
D 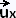 f(x) = lim (f(x + αh) - f(x))/h f(x) = lim (f(x + αh) - f(x))/h
h → 0
Similarly,
The derivative of a function of two variables is its rate of change with x and y, defined by :
Df(x,y) =
lim (f(x + αh, y + βh) - f(x,y))/h
h → 0
Written as
D  f(x,y) =
lim (f(x + αh, y + βh) - f(x,y))/h f(x,y) =
lim (f(x + αh, y + βh) - f(x,y))/h
h → 0
The definition of the directional derivative is :
The rate of change of f(x,y) in the direction of the unit vector  = 〈α, β〉 is called the directional derivative, denoted by
D = 〈α, β〉 is called the directional derivative, denoted by
D  f(x,y) and defined by f(x,y) and defined by
D  f(x,y) =
lim (f(x + αh, y + βh) - f(x,y))/h f(x,y) =
lim (f(x + αh, y + βh) - f(x,y))/h
h → 0
3. Explicite form of the directional derivative
We want to write down a formula much simpler to use
than the limit definition presented above.
Let�s define a new function of a single variable of z
g(z) = f(xo + αz, yo + βz)
By the definition of the derivative for functions of a single variable we have:
g'(z) = lim (g(z + h) - g(z))/h
h → 0
g'(0) = lim (g(h) - g(0))/h
h → 0
We have
g(h) = f(xo + αh, yo + βh),
g(0) = f(xo, yo)
Therefore
g'(0) = lim (f(xo + αh, yo + βh))/h = D  f(xo,yo) f(xo,yo)
h → 0
So
g(z) = f(x,y) = f(xo + αz, yo + βz),
where x = xo + αz , and y = yo + βz
Using the chain rule, we have
g'(z) = dg(z)/dz = (∂f/∂x)(dx/dz) + (∂f/∂y)(dy/dz)
=
(∂f/∂x)(α) + (∂f/∂y)(β)
=
αfx + βfy
g'(z) = αfx(x,y) + βfy(x,y)
So,taking z = 0, we obtain
g'(0) = D f(xo,yo) =
αfx(xo,yo) + βfy(xo,yo) f(xo,yo) =
αfx(xo,yo) + βfy(xo,yo)
Hence, for any x and any y, we have the following formula:
g'(z) = D f(x,y) =
αfx(x,y) + βfy(x,y) f(x,y) =
αfx(x,y) + βfy(x,y)
D f(x,y) =
αfx + βfy f(x,y) =
αfx + βfy
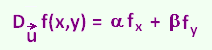
Working with functions with more than two variables, the
formula to use is similar to found for function with two variables.
For instance, the directional derivative of f(x,y,z) in the direction of the unit vector  (α β γ) is given by, (α β γ) is given by,
D f(x,y,z) =
αfx + βfy + γfz f(x,y,z) =
αfx + βfy + γfz
Example
Find the directional derivative D  f(0,1), where f(x,y) = 2 xy , and f(0,1), where f(x,y) = 2 xy , and
 is the unit vector in the direction
θ = π/4. is the unit vector in the direction
θ = π/4.
 =
〈cos (π/4), sin (π/4) 〉 =
〈√2/2, √2/2 〉 =
〈cos (π/4), sin (π/4) 〉 =
〈√2/2, √2/2 〉
fx = 2y, and fy = 2x.
Then
D  f(x,y) =
αfx + βfy =
(√2/2) 2y + (√2/2) 2x =
√2(x + y) f(x,y) =
αfx + βfy =
(√2/2) 2y + (√2/2) 2x =
√2(x + y)
D  f(x,y) =
√2(x + y)
. Therefore f(x,y) =
√2(x + y)
. Therefore
D  f(0,1) =
√2(x + y) = √2. f(0,1) =
√2(x + y) = √2.
D  f(0,1) = √2. f(0,1) = √2.
4. Other formula for the directional derivative
D f(x,y,z) =
αfx + βfy + γfz f(x,y,z) =
αfx + βfy + γfz
This expression of the directional derivative can be written as the dot product of ∇f and  : :
D f(x,y,z) =
∇f . f(x,y,z) =
∇f . 
 is the unit vector that gives the direction of change = 〈α,β,,γ〉. is the unit vector that gives the direction of change = 〈α,β,,γ〉.
∇f is the gradient vector of f(x,y,z) = 〈fx,fy,fz〉
5. Naximum rate of change of a function
D f(x,y,z) =
∇f . f(x,y,z) =
∇f .
Takinng the magnitude of this dot poduct and because
the directional vector  is a unit vector, we have: is a unit vector, we have:
||D f(x,y,z) =
∇f . f(x,y,z) =
∇f . || = || =
||∇f|| || || cos φ =
||∇f|| cos φ . || cos φ =
||∇f|| cos φ .
φ is the angle between ∇f and  . .
||D f(x,y,z) =
||∇f|| cos φ f(x,y,z) =
||∇f|| cos φ
The largest possible value of φ is 0. This is the direction that we need to move in order to achieve that maximum rate of change.  will point in the same direction as the gradient ∇f. will point in the same direction as the gradient ∇f.
The maximum rate of change of the function f(x,y,z), that is
the maximum value of D f(x,y,z) is given by ||∇f|| and occur in the direction of ∇f. f(x,y,z) is given by ||∇f|| and occur in the direction of ∇f.
|
|