Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Partial Derivatives
Derivatives of functions of more than one variable
Higher Order Partial Derivatives
1. Defnitions and rules
As we had higher order ordinary derivatives with functions of one variable,
we will also have higher order partial derivatives of functions of more than
one variable. We will consider the case of a function of two variables f(x,y).
The first order partial derivatives with respect to x and with
respect to y, of the function f(x,y) are in turn differentiated
each with respect to x or y. Here for the case of a function of two
variables there will be a total of four possible second order derivatives.
Here they are:
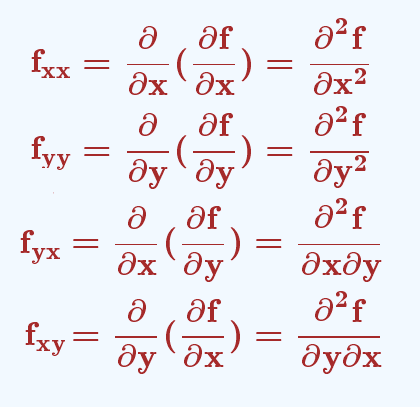
2. Example
Find all the four second order derivatives for f(x,y) = cos(x) + xy3
We have:
fxx = - cos(x) ,
fyy = 6xy ,
fyx = 3y2 , and
fxy = 3y2 .
Let�s notice that fxy = fyx . This is not always the case.
fxy and fyx are equals following the Clairaut�s Theorem:
Let f(x,y) a function defined on a disk D that contains the point (a, b). If the functions
fxy and fyx are continuous on this disk then
fxy(a,b) = fyx(a,b)
Alexis Claude Clairaut (1713 � 1765) French mathematician.
3. Hier order derivatives
Here are some third order partial derivatives of function of two variables:
fxxx, fxyy , fxxy, fxyx ,
fyxx ...
For these we differentiate once with respect to y and twice with respect to x,
the extension to Clairaut�s Theorem says these functions are equals. That is
fxxy = fxyx = fyxx
We can extend Clairaut�s theorem to any function and mixed partial derivatives.
The only requirement is that in each derivative we differentiate with respect
to each variable the same number of times. For example:
fxxxxtyy = ftyyxxxx
The ScientificSentence
|
|