Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Integrals
Change of variables
Jacobian of a transformation
1. Definitions
The substitution rule in integral:
∫ab f(g(x)) dg(x) = ∫cd f(u) du
where
dg(x) = g'(x) dx and u = g(x)
used in one-dimension holds in
two-dimensions and three-dimensions integrals.
For a function, the set of equations u = g(x) that define the change of variables
are called the transformation .
The change of variables is maily used to get the related calculus
easier. For example converting double integrals to polar coordinates
or triple integrals to cylindrical or spherical coordinates.
The change of variables in integrals involve the conversion of the region,
over we integrate, the fonction itself, and the differential element.
2. Examples: Change in the region of integration :
xy-coordinates → uv-coordinates
Example 1
The region R, over we want to integrate, is an ellipse defined
by x2 + y2/16 = 1.
We want to determine the new region of R due to the given transformation
x = u/2 and y = 2v.
Substituting x anf y in the equation yields:
u2/4 + v2/4 = 1
u2 + v2 = 4
This change of variables transforme the ellipse to a disk of radius 2.
Example 2
The region R, over we want to integrate, is a triangle
delimited by the three lines y = - x + 1, y = 2x - 2, and
y = x + 1.
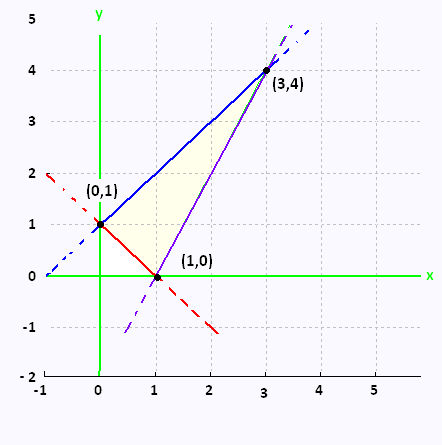
We want to determine the new region of R due to the given transformation
x = (u + v)/2 and y = (u - v)/2 .
Substituting x anf y in the three equations yields:
y = - x + 1
(u - v)/2 = - (u + v/2 + 1
u - v = - u - v + 2
u = 1
y = 2x - 2
(u - v)/2 = (u + v) - 2
u - v = 2u + 2v - 4
u + 3 v = 4
v = - u/3 + 4/3
y = x + 1.
(u - v)/2 = (u + v)/2 + 1
u - v = u + v + 2
v = - 1
This change of variables transform the triangle
to a right triangle .
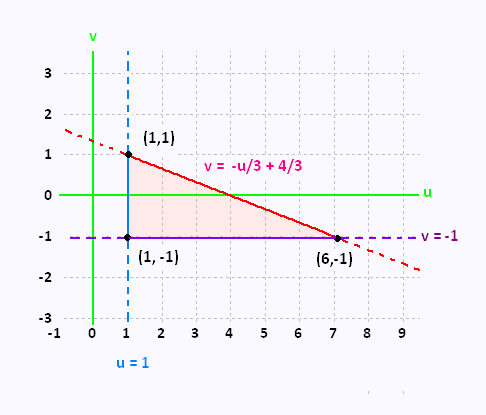
3. Jacobian of the differential element
3.1. Double integral
The Jacobian of the transformation:
x = g(u,v)
y = h(u,v)
is:
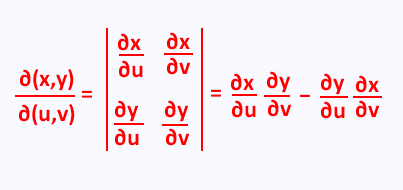
The change of variables for a double integral over the region R, under
the transformation x = g(u,v) , y = h(u,v), becomes the
integral over S as follows:
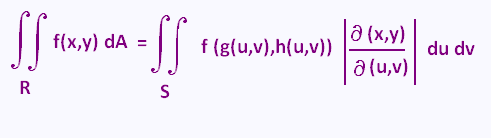
Notice that, now, we are integrating with respect to u and v.
Also note that we are taking the absolute value of the Jacobian.
The relationship between the differentials dA and du dv is :
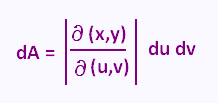
Example 3:
Show that the changing from the cartesian coordinates to
polar coordinates is dA = r dr dθ.
The transformation is : x = r cos θ , y = r sin θ .
u = r
v = θ
∂x/∂u = cos θ
∂x/∂v = - r sin θ
∂y/∂u = sin θ
∂y/∂v = r cos θ
The Jacobian for this transformation is :
(cos θ)(r cos θ) - (sin θ)(- r sin θ) =
r cos2 θ + r sin2 θ = r
Therefore
dA = Jacobian dr dθ = r dr dθ
The differential element in polar coordinates is :
dA = r dr dθ
Example 4
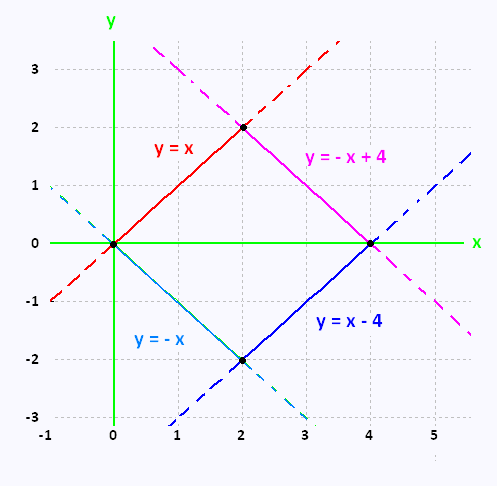
The region R, over we want to integrate, is a trapezoidal region
having the four vertices (0,0), (2,2), (2, -2) and (4,0).
The related lines have the equations:
y = x ,
y = - x ,
y = x - 4 , and
y = - x + 4
a) Determine the new region of R due to the given transformation
x = 2u - 3v and y = 2u + 3v .
b) Evaluate ∫∫R (x - y) dA
a) Substituting x anf y in the three equations yields:
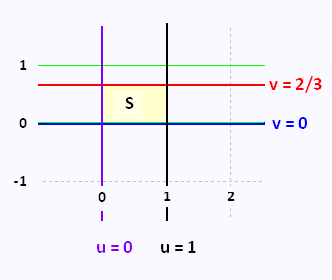
y = x → 2u + 3v = 2u - 3v → v = 0
y = - x → 2u + 3v = - 2u + 3v → u = 0
y = x - 4 → 2u + 3v = 2u - 3v - 4 → v = 2/3
y = - x + 4 → 2u + 3v = - 2u + 3v + 4 → u = 1
This change of variables transform the trapezoidal region
to a rectangle.
∂x/∂u = 2
∂x/∂v = - 3
∂y/∂u = 2
∂y/∂v = 3
The Jacobian for this transformation is :
(3)(3) - (2)(- 3) = 9 + 6 = 15
The differential element becomes:
dA = 15 du dv
b)
Here are the limits of integration:
0 ≤ u ≤ 1
0 ≤ v ≤ 2/3
∫∫R f(x,y) dA =
∫∫S 15 f(u,v) du dv
∫∫R (x - y) dA =
∫∫S 15 [(2u - 3v) - (2u + 3v)] du dv =
∫∫S 15 (- 6 v) du dv =
∫∫S 15 (- 6 v) du dv =
- 90 ∫02/3
∫01 v du dv =
- 90 ∫02/3
(1) v dv =
- 90 (1) ((2/3)2/2) = - 90 (4/9) (1/2) = - 20
∫∫R f(x,y) dA = - 20
Example 5
Evaluate ∫∫R x2 - xy + y2 dA,
where R is the ellipse of equation x2 - xy + y2 = 4,
and using the transformation:
x = u - v/√3
y = u + v/√3
First, we transforme first f(x,y) = x2 - xy + y2.
x2 - xy + y2 = (x - y)2 + xy
= (- 2v/√3)2 + (u - v/√3)(u + v/√3) =
4v2/3 + u2 - (v/√3)2 =
4v2/3 + u2 - v2/3 =
u2 + v2
x2 - xy + y2 = u2 + v2
R is transformed into a circle of radius r = 2.
∂x/∂u = 1
∂x/∂v = - 1/√3
∂y/∂u = 1
∂y/∂v = 1/√3
The Jacobian for this transformation is :
(1)(1/√3) - (1)(- 1/√3) = 2/√3.
The differential element becomes:
dA = (2/√3) du dv
Therefore, the integral becomes:
∫∫R x2 - xy + y2 dA =
∫∫S u2 + v2 (2/√3) du dv
The second change into polar coordinates u r cos θ v = r sin θ leads to:
∫∫S r2 (2/√3) r dr dθ =
∫02π ∫02 r3 (2/√3) dθ =
∫02π (24/4) (2/√3) dθ =
(24/4) (2/√3) 2π = 16 π/√3
∫∫R x2 - xy + y2 dA = 16 π/√3
3.2. Triple integral
We will use the transformation x = g(u,v,w), h(u,v,w), k(u,v,w) , and
transform the region R into the new region S.
To do the integral, we will need a Jacobian. Here is the definition of
the Jacobian in three-dimentional space for this transformation.

The change of variables for a triple integral over the region R, under
the transformation x = g(u,v,w), y = h(u,v,w), z = k(u,v,w) , becomes the
integral over S as follows:

Notice that, now, we are integrating with respect to u , v, and w.
Also note that we are taking the absolute value of the Jacobian.
The relationship between the differentials dV and du dv dw is :
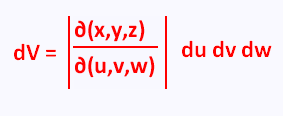
The transformation is : x = r sin θ cos φ ,
y = r sin θ sin φ , z = r cos θ.
u = r
v = θ
w = φ
∂x/∂u = sin θ cos φ
∂x/∂v = r cos θ cos φ
∂x/∂w = - r sin θ sin φ
∂y/∂u = sin θ sin φ
∂y/∂v = r cosθ sin φ
∂y/∂v = r sin θ cos φ
∂z/∂u = cos θ
∂z/∂v = - r sin θ
∂z/∂v = 0
The Jacobian for this transformation is :
|
sin θ cos φ | r cos θ cos φ | - r sin θ sin φ |
|
sin θ sin φ | r cosθ sin φ | r sin θ cos φ |
|
cos θ | - r sin θ | 0
|
=
(sin θ cos φ)[(0) - (r sin θ cos φ)(- r sin θ )] +
(r cos θ cos φ )[( r sin θ cos φ )(cos θ ) - (0)] +
(- r sin θ sin φ )[(sin θ sin φ)(- r sin θ ) - (cos θ)(r cosθ sin φ )]
=
r2 sin θ cos φ sin2 θ cos φ +
r2 cos2 θ cos2 φ sin θ +
(r2 sin θ sin2 φ ) [sin2 θ + cos2 θ] =
r2 sin θ[
cos2 φ (sin2 θ +
cos2 θ ) +
sin2 φ
]
=
r2 sin θ[
cos2 φ +
sin2 φ
]
=
r2 sin θ
Then
Jacobian = r2 sin θ
Therefore
dA = Jacobian . dr dθ dφ = r2 sin θ dr dθ dφ
The differential element in spherical coordinates is :
dA = r2 sin θ dr dθ dφ
|
|