Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Line integrals with respect to arc length ds
1. Definition and method
Integrating a function of a single variable f(x) over an interval [a,b], x takes all the values in this interval starting at a and ending at b.
Double-integrating a function of a two variable f(x,y) over a domain [a,b] D, x and y take all the values in this domain starting at a and ending at b for x; and starting atc and ending at d for y.
With line integrals we integrate the function f(x,y), a function of two variables, and the values of x and y will be the points, (x,y), that lie on a curve C.
Notice that this is different from the double integrals where the integration is made over a region R or D. In line integrals, we integrate over a curve made from the points of the the
function itself.
Let�s consider the curve C that the points come from, and assume assume that the curve is smooth. The curve is given by the parametric equations:
x = g(t), y = h(t) a ≤ t ≤ b
With the parameterization of the curve as a vector function,
the curve is given by:
 (t) = g(t) (t) = g(t) + h(t) + h(t) a ≤ t ≤ b a ≤ t ≤ b
Let's recall that the curve is called smooth if (t) is continuous and (t) is continuous and (t) ≠ (t) ≠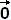 for all t. for all t.
The line integral of f(x,y) along C is denoted by:
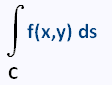
The differential element is ds. This is the fact that we are moving along the curve, C, instead dx for the x-axis, or dy for
the y-axis.
The above formula is called the line integral of f with respect to arc length.
Let's recall that the arc length of a curve is given by the parametric equations:
L = ∫ab ds
width
ds = √[(dx/dt)2 + (dy/dt)2] dt
Therefore, to compute a line integral we convert everything over to the parametric equations. The line integral is then:
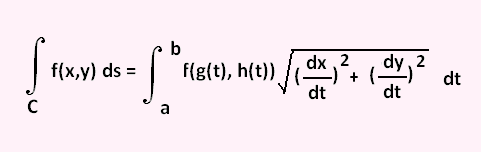
Example 1
Evaluate ∫C 3x2 ds where C is the line segment from (-1, 1) to (1,2).
We have already seen, in the equation of a line in 3D space section, that the parameterization formula of the line segment
starting at the point(xo, yo) and ending at the point (x1,y1) is :
 (t) = (1 - t) 〈xo, yo〉 +
t 〈x1,x2〉 (t) = (1 - t) 〈xo, yo〉 +
t 〈x1,x2〉
That is:
x = xo (1 - t) + x1 t
y = yo (1 - t) + y1 t
So, the parameterization formula of the line segment starting at (-1, -1) and ending at (1,2) is :
 (t) = (1 - t) 〈-1, 1〉 +
t 〈1,2〉. (t) = (1 - t) 〈-1, 1〉 +
t 〈1,2〉.
That is:
x = (1 - t) (- 1) + t(1) = 2t - 1
y = (1 - t) (1) + t(2) = t + 1
At (-1, 1): x = - 1, y = 1 → t = 0 , and
at (1,2): x = 1 , y = 2 → t = 1
so 0 ≤ t ≤ 1
We have:
dx/dt = 2 , and
dy/dt = 1.
Hence:
ds = √[22 + 12] dt = √5 dt.
ds = √5 dt
Therefore
∫C 3x2 ds = ∫01 3(2t - 1)2 √5 dt =
3 √5 ∫01 (4t2 - 4t + 1) dt =
3√5 [(4/3)t3 - 2t2 + t] 01 =
3√5 [(4/3) - 2 + 1] =
3√5 [1/3] =
√5
∫C 3x2 = √5
Example 2
Evaluate ∫Cxy2 ds where C is the right half of the circle x2+ y2 = 16, rotated in the counter clockwise direction.
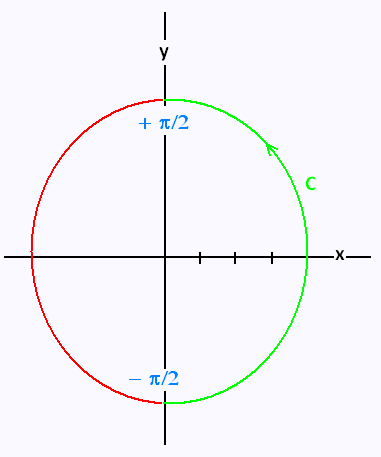
We parameterize the curve which is the circle, then the integrand, and then the differial element:
x = 4 cos t, y = 4 sin t - π/2 ≤ t ≤ + π/2.
f(x,y) = xy2 = 4 cos t (4 sint)2 =
64 cos t sin2t
dx/dt = - 4 sin t , dy/dt = 4 cos t
ds = 4 dt
Therefore
∫C xy2 ds =
∫- π/2 + π/2
64 cos t sin2t (4 dt) =
256 ∫- π/2 + π/2
cos t sin2t dt =
256 [(1/3) sin3 t]- π/2 + π/2 =
(256/3)[sin3 (π/2) - sin3 (-π/2)] =
2 (256/3) sin3 (+ π/2) = 2 (256/3) = 512/3.
∫C xy2 ds = 512/3
2. Integrals over piecewise smooth curves
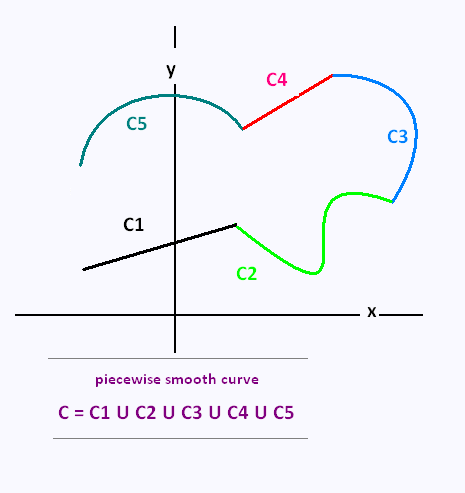
Now, we are going to integrate line integrals over piecewise smooth curves.
A piecewise smooth curve C is any curve that can be written as the union of a finite number of smooth curves, C1, C2, C3, , ... Cn,
where the end point of Ci is the starting point of Ci+1.
To evaluate the line integrals over piecewise smooth curves , we evaluate the line integral over each of the pieces and then add them up:
∫C f(x,y) ds =
∫C1 f(x,y) ds ∫C2 f(x,y) ds
∫C3 f(x,y) ds ∫C4 f(x,y) ds
∫C5 f(x,y) ds + ...
Example 3
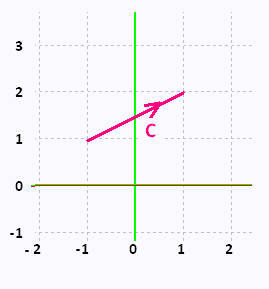
Evaluate ∫C 2x ds
where C is the curve shown below.
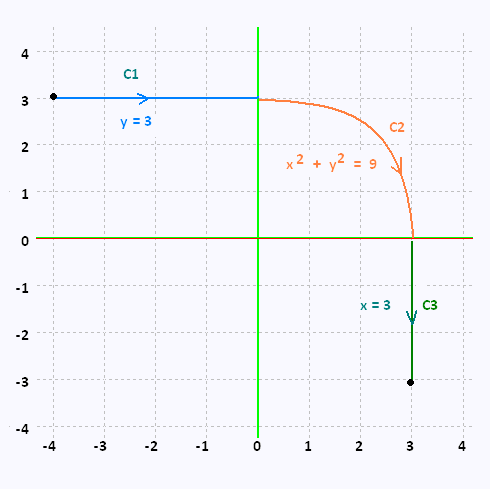
C1: x = t , y = 3
- 4 ≤ t ≤ 0
C2: x = 3 cos t , y = 3 sin t
π/2 ≤ t ≤ 0
C3: x = 3 , y = t
- 3 ≤ t ≤ 0
C1:
dx/dt = 1 dy/dt = 0
ds = dt
∫C1 2x ds = ∫- 40 2t dt =
(t2)|- 40 = 16
∫C1 2x ds = 16
C2:
dx/dt = - 3 sint dy/dt = 3 coos t
ds = 3 dt
∫C2 2x ds = ∫π/20 2 cos t (3 dt) =
6 (sin t)|π/20 =
6 (sin t)|π/20 = - 6
∫C2 2x ds = - 6
C3:
dx/dt = 0 dy/dt = 1
ds = dt
∫C3 2x ds = ∫0-3 2 (3) dt =
6 (t)|0-3 = 6(- 3) = - 18
∫C3 2x ds = - 18
Therefore:
∫C 2x ds =
∫C1 2x ds +
∫C2 2x ds +
∫C3 2x ds .
=
16 - 6 - 18 = - 8
∫C 2x ds = - 8
Example 4
In the example 1, we have have found:
∫C 3x2 ds where C is the line segment from (-1, 1) to (1,2).
Here we switch the direction of the curve to see whether
le liine integral change:
We evaluate Then ∫-C 3x2 ds where -C is the line segment from (1,2) (- 1, 1).
The parameterization formula of the line segment starting at (1, 2) and ending at (- 1, 1) is :
 (t) = (1 - t) 〈1, 2〉 +
t 〈- 1,1〉. (t) = (1 - t) 〈1, 2〉 +
t 〈- 1,1〉.
That is:
x = (1 - t) (1) + t(- 1) = 1 - 2t
y = (1 - t) (2) + t(1) = 2 - t
At (1,2): x = 1 , y = 2 → t = 0 , and
At (-1, 1): x = - 1, y = 1 → t = 1
so 0 ≤ t ≤ 1
We have:
dx/dt = - 2 , and
dy/dt = - 1.
Hence:
ds = √[22 + 12] dt = √5 dt.
ds = √5 dt
Therefore
∫-C 3x2 ds = ∫01 3(1 - 2t)2 √5 dt =
√5
∫-C 3x2 = √5 , as in the example 1.
So, for this kind of line integrals, that is for the integrals with respect to the
arc length ds , when we switch the direction of the curve, the line integral (with respect to arc length) will not change. But it does not hold for all the line integrals.
For a line integrals with respect to arc length, we have:
∫C f(x,y) ds = ∫-C f(x,y) ds
3. Line integrals over a three-dimensional curve
The line integrals over a three-dimensional curve can be extended from the
line integrals over atwo-dimensional curve.
Let�s suppose that the three-dimensional curve C is given by the
parameterization:
x = x(t), y = y(t), z = z(t) a ≤ t ≤ b.
The line integral is then given by:
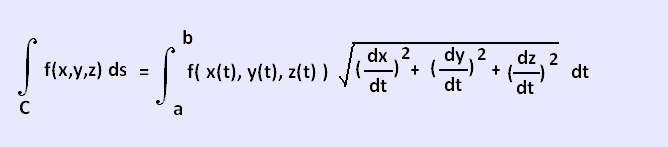
|
|