Calculus III:
Partial Derivatives
Derivatives of functions of more than one variable
Changing one of the variables
First order partial derivatives.

1. Defnitions and rule

Recall that, given a function of one variable, f(x) , its derivative, f'(x), represents the rate of change of the function as x changes.

For functions of more than one variable, one can change only one, or more than one variables.

Partial derivative means changing one of the variables at a time, while the remaining variable(s) are held fixed.

Just as with functions of one variable, we can have first order partial derivatives, as well as derivatives of all orders.

With functions of a single variable f(x), we denote the derivative with a single prime f'(x). However, with partial derivatives we, need to specify the variable that we are differentiating with respect to.
We subscript the variable that we differentiate with respect to f_x(x,y).

Here is the rule:

To compute f_x(x,y), we treat all the y’s as constants (or numbers) and then differentiate the x’s. Likewise, to compute f_y(x,y), we treat all the x’s as constants and then differentiate the y’s as we are used to doing.

f(x) → f'(x) = df/dx (ordinary derivative)

f(x,y) → f_x(x,y) = ∂f(x,y)/∂x, and
f_y(x,y) = ∂f(x,y)/∂y (partial derivative)

2. Changing one of the variables

Let's take the following example: f(x, y) = 2 x²y³

Let’s start with the function and let’s determine the rate at which the function is changing at a point, (a, b) , if we hold y fixed and allow x to vary and if we hold x fixed and allow y to vary.

• First case: Holding y fixed and allowing x to vary.

If we hold y fixed and allow x to vary, the rate of change of the function f(x, y) at the point (a, b) will involve only the variable x, and y remains equal to b. So we get then a new function of a single variable:

g(x) = 2b³ x²

Therefore, the rate of change of f(x,y) at (a,b) is the rate of change of g(x) at the point x = a, that is g'(a).

For this function of a single variable , we know how to derive:

g'(a) = 4b³ x

This is called the partial derivative of f(x,y) with respect to x at the point (a,b) .

We write:

f_x(a,b) = ∂f(x,y)/∂x = 4 a b³

• Second case: Holding x fixed and allowing y to vary.

In a similar way,

If we hold x fixed and allow y to vary, the rate of change of the function f(x, y) at the point (a, b) will involve only the variable y, and x remains equal to a. So we get then a new function of a single variable:

h(x) = 2a² y³

Therefore, the rate of change of f(x,y) at (a,b) is the rate of change of h(x) at the point y = b, that is h'(y).

For this function of a single variable , we know how to derive:

g'(b) = 6 a² b²

This is called the partial derivative of f(x,y) with respect to y at the point (a,b) .

We write:

f_y(x,y) = ∂f(x,y)/∂y = 6 a² b²

Using the standard notion, we have then:

f_x(x,y) = ∂f(x,y)/∂x = 4xy³
f_y(x,y) = ∂f(x,y)/∂y = 6x²y²

3. Formal definition of the partial derivative

The definition of f_x(x,y) and f_y(x,y)is similar to the definition of the derivative for single variable functions.

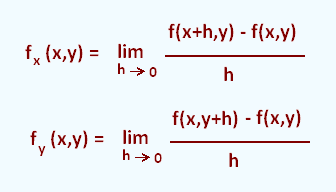
4. Examples

Example 1

f(x,y) = 2x²y + y

f_x(x,y) = ∂f(x,y)/∂x = 4xy
f_y(x,y) = ∂f(x,y)/∂y = 2x² + 1

Example 2

Find ∂y/∂x for 2y³ + x² = 3x

6y² ∂y/∂x + 2x = 3

∂y/∂x = (3 - 2x)/ 6y²