Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Vector functions
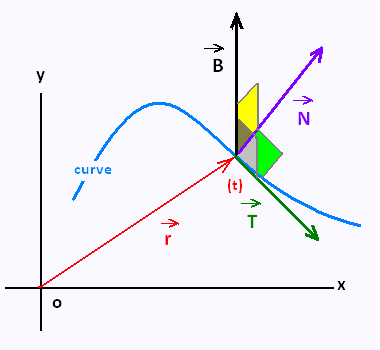
Tangent vectors
Normal vectors
Binormal vectors
1. Tangent vector
Here are some applications of the derivative of vector functions.
We have seen that the derivative of a function of one-variable is
is the slope of the tangent line on the curve of this function at a
certain point.
With vector functions, the result is the same.
Given a vector function,  (t) , its derivative (t) , its derivative  (t) is called the tangent vector . (t) is called the tangent vector .
The tangent line to  (t) at a point P is the line that passes through the point P and is parallel to the tangent vector (t) at a point P is the line that passes through the point P and is parallel to the tangent vector  (t). (t).
Notice that this vector must be non zero:
 (t) ≠ (t) ≠  . .
Therefore, the unit tangent vector to the curve is given by:
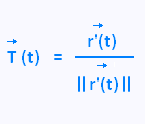
Example
Let's consider the following vector function:
 (t) = (t2, t, 2t) (t) = (t2, t, 2t)
So  (t) = 〈 2t, 1, 2 〉 (t) = 〈 2t, 1, 2 〉
The length of the tangent vector is:
|| (t)|| = sqrt((2t)2 + 12
+ 22) = √(4t2 + 5) (t)|| = sqrt((2t)2 + 12
+ 22) = √(4t2 + 5)
Therefore
The unit tangent vector = 〈 2t, 1, 2 〉 /√(4t2 + 5)
=
(2t/√(4t2 + 5)) + (1/√((4t2 + 5)) + (1/√((4t2 + 5)) + (2/√(4t2 + 5)) + (2/√(4t2 + 5))
2. Normal vector
The unit normal vector is defined to be:
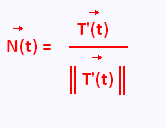
The tangent vector  (t) is parallel to the line that passes through a point defined by the vector function (t) is parallel to the line that passes through a point defined by the vector function  (t). (t).
The derivative of the tangent vector  '(t) is
perpendicular to the vector tangent '(t) is
perpendicular to the vector tangent  (t). (t).
Therefore the derivative  (t) of
the vector tangent (t) of
the vector tangent  (t) is perpendicular to the
vector tangent (t) is perpendicular to the
vector tangent  (t). (t).
The unit normal vector  (t) is perpendicular to the unit tangent vector (t) is perpendicular to the unit tangent vector  (t) and hence to the curve . (t) and hence to the curve .
3. Binormal vector
The binormal vector is defined as:
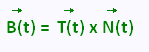
That is the cross product of the unit tangent and unit normal vector.
It is then orthogonal to both the tangent vector and the normal vector.
Example
Find the binormal vector of the vector function
 (t) =
〈 t, sin t, cos t 〉 (t) =
〈 t, sin t, cos t 〉
 (t) = 〈 1, cos t, - sin t 〉 /
√2 (t) = 〈 1, cos t, - sin t 〉 /
√2
 (t) = 〈 0, - sin t, - cos t 〉 /1 = = 〈 0, - sin t, - cos t 〉 (t) = 〈 0, - sin t, - cos t 〉 /1 = = 〈 0, - sin t, - cos t 〉
 (t) = (t) =  (t) x (t) x  (t) = (t) =
(1/√2)〈 - cos2 - sin2(t)),
0 + cos t, - sin t - 0 〉 =
= (1/√2) 〈 - 1, cos t, - sin t 〉
 (t) = (1/√2) 〈 - 1, cos t, - sin t 〉 (t) = (1/√2) 〈 - 1, cos t, - sin t 〉
|
|