SPHERICAL COORDINATES

1. The basic relationships

The folowing figure gives the spherical coordinates of a point P , that is of a vector in space:



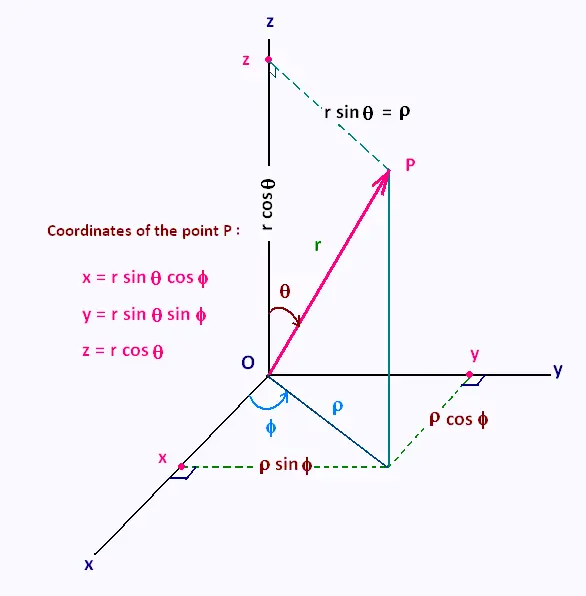
We have the following relationships:

r = [x² + y² + z²]^1/2
tg θ = sin θ/cosθ = (ρ/r)/(z/r) = [x² + y²]^1/2/z
tg φ = y/x

r goes from : 0 to ∞ ( in the space)
θ goes from 0 to π (along the z-axis)
φ goes from 0 to 2π (over the xy-plane)


2. Unit vectors transformatins:


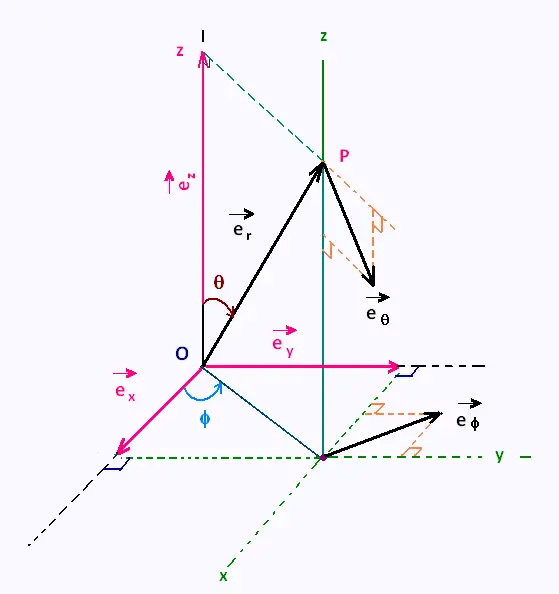
We have the following relationships:

e_x = sinθcosφ e_r + cosθcosφ e_θ - sinφ e_φ
e_y = sinθsinφ e_r + cosθsinφ e_θ + cosφ e_φ
e_z = cosθ e_r - sinθ e_θ

Writing these relations using a matrix, we obtain

[e_x, e_y, e_z] = M [e_r, e_θ, e_φ]

Matrix M =


The transformation is obtained by using the related inverse matrix: :

[e_r,e_θ, e_φ] = M^-1[e_x, e_y, e_z]

Matrix M^-1 =


Therefore:

e_r = sinθcosφ e_x + sinθsinφ e_y + cosθ e_z
e_θ = cosθcosφ e_x + cosθsinφ e_y - sinθ e_z
e_φ = - sinφ e_x + cosφ e_y



3. The components of the gradiant ∇

We will express the components of the gradiant (∂/∂x , ∂/∂y , ∂/∂z) in the cartesian system according to the ones in the spherical system:

x is a function of r, θ and φ
y is a function of r, θ and φ
z is a function of r and θ

Hence:

∂/∂x

∂/∂x = (∂/∂r) ∂r/∂x + (∂/∂θ) ∂θ /∂x + (∂/∂φ) ∂φ/∂x ∂r/∂x = (1/2) (1/r) 2. x = x/r = ρ cos φ/r = sin θ cos φ

• ∂θ /∂x = (1/cos² θ) ∂θ/∂x = (1/z) (1/2) (1/ρ) 2. x = x /ρz = cos φ /z = cos φ /r cos θ

∂θ/∂x = cos φcosθ/r

• ∂φ/∂x = (1/cos² φ) ∂φ/∂x = - y/x² = -sinφ/ρcos² φ

∂φ/∂x = - sinφ/ρ

Therefore:

∂/∂x = sin θcos φ (∂/∂r) +
cos φcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)

∂/∂y

∂/∂y = (∂/∂r) ∂r/∂y + (∂/∂θ) ∂θ /∂y + (∂/∂φ) ∂φ/∂y

• ∂r/∂y = (1/2) (1/r) 2. y = y/r = ρsin φ/r = sin θsin φ

∂r/∂y = sin θsin φ

• ∂θ /∂y = (1/cos² θ) ∂θ/∂y = (1/z) (1/2) (1/ρ) 2.y =
y /ρz = sin φ /z = sin φ /r cos θ

∂θ/∂y = sin φcosθ/r

∂φ/∂y = (1/cos² φ) ∂φ/∂y = 1/x = 1/ρcos φ = 1/r sinθcos φ

∂φ/∂y = cos φ/r sinθ

Therefore:

∂/∂y = sin θsin φ (∂/∂r) +
sin φcosθ/r (∂/∂θ) + cos φ/r sinθ (∂/∂φ)

∂/∂z

∂/∂z = (∂/∂r) ∂r/∂z + (∂/∂θ) ∂θ/∂z

• ∂r/∂z = (1/2) (1/r) 2. z = z/r = cos θ

∂r/∂z = cos θ

• ∂θ/∂z = (1/cos² θ) = - ρ/z² = - ρ/r² cos²θ

∂θ/∂z = - ρ/r² = - sinθ/r

Therefore:

∂/∂z = cos θ (∂/∂r) - sinθ/r (∂/∂θ)

To recap:

∂/∂x = sin θcos φ (∂/∂r) + cos φcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)

∂/∂y = sin θsin φ (∂/∂r) + sin φcosθ/r (∂/∂θ) + cos φ/r sinθ (∂/∂φ)

∂/∂z = cos θ (∂/∂r) - sinθ/r (∂/∂θ)


4. The Laplacien: Δ

∂²/∂x² = (∂/∂x)(∂/∂x) = [sin θcos φ (∂/∂r) + cos φcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)] [sin θcos φ (∂/∂r) + cos φcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)]

= (sin θcos φ)[∂/∂r][sin θcos φ (∂/∂r) + cosφcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)] + (cosφcosθ/r)[∂/∂θ][sin θcos φ (∂/∂r) + cosφcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)] - (sinφ/ρ)[∂/∂φ][sin θcos φ (∂/∂r) + cosφcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ)]

= (sin² θcos² φ)(∂²/∂r²) - (sin θcos² φcosθ/r²) (∂/∂θ) + (cos φsinφ/r²) (∂/∂φ) + + (cos²φcos ²θ/r) (∂/∂r) - cos²φsinθcosθ/r² (∂/∂θ) + cos²φcos²θ/r² (∂²/∂θ²) + cosφsinφcos²θ/r²sin²θ) ∂/∂φ +(sinθ sin²φ/rsinθ)∂/∂r + (sin²φcosθ/r²sinθ) ∂/∂θ + (sinφcosφ/r²sin²θ)∂/∂φ + (sin²φ/r²sin²θ)∂²/ ∂φ²

∂²/∂y² = ∂/∂y(∂/∂y) = [sin θsin φ (∂/∂r) + sin φcosθ/r (∂/∂θ) + cos φ/r sinθ (∂/∂φ)] [sin θsin φ (∂/∂r) + sin φcosθ/r (∂/∂θ) + cos φ/r sinθ (∂/∂φ)]

= (sin² θcos² φ)(∂²/∂r²) - (cosθsin² φsinθ/r²) (∂/∂θ) - (cos φsinφ/r²) (∂/∂φ) + + (sin²φcos ²θ/r) (∂/∂r) - sin²φsinθcosθ/r² (∂/∂θ) + sin²φcos²θ/r²(∂²/ ∂θ²) - sinφcosφcos²θ/r²sin²θ) ∂/∂φ +(sinθ cos²φ/rsinθ)∂/∂r + (cos²φcosθ/r²sinθ) ∂/∂θ - (sinφcosφ/r²sin²θ)∂/∂φ + (cos²φ/r²sin²θ)∂²/ ∂φ²

∂²/∂z² = [∂/∂z][∂/∂z]= [cos θ (∂/∂r) - sinθ/r (∂/∂θ)] [cos θ (∂/∂r) - sinθ/r (∂/∂θ)] = cos²θ∂²/∂r² + (sinθcosθ/r²)∂/∂θ + (sin²/r)∂/∂r + (sin²/r²) ∂²/∂θ² + (sinθcosθ/r²)∂/∂θ

Therefore:

Δ = ∂²/∂r² +(2/r) ∂/∂r + (1/r²)(sinθ/cosθ)∂/∂θ + (1/r²) ∂²/∂θ² + (1/r²sin² θ)∂²/∂φ²

Or:

Δ = (1/r²)∂/∂r(r² ∂/∂r) + (1/r²sinθ)∂/∂θ(sinθ∂/∂θ) + (1/r²sin²θ)∂²/∂φ²)



5. Volume element:

From the following figure:



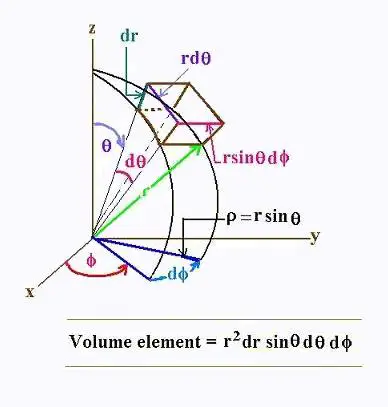
We obtain: dV = r²drsinθdθdφ



6. The solid angle:

The related solid angle is, by definition, equal to the lateral surface over the square of fthe radius. That is:
dΩ = rdθ rsinθdφ /r² = sinθdθdφ

dΩ =sinθdθdφ

Ω = ∫dΩ = 2π∫sinθdθ =
2π∫[-cosθ] ( from 0 to π) = 4π


7. The operator DEL

We have: ∇ = ∂/∂x e_x + ∂/∂y e_y + ∂/∂z e_z.
And:

e_x = sinθcosφe_r + cosθcosφe_θ - sinφ e_φ e_y = sinθsinφ e_r + cosθsinφe_θ + cosφe_φ e_z = cosθe_r - sinθe_θ
And:

∂/∂x = sin θcos φ (∂/∂r) + cos φcosθ/r (∂/∂θ) - sinφ/ρ (∂/∂φ) ∂/∂y = sin θsin φ (∂/∂r) + sin φcosθ/r (∂/∂θ) + cos φ/r sinθ (∂/∂φ) ∂/∂z = cos θ (∂/∂r) - sinθ/r (∂/∂θ)

Therefore:

∇ = sin θ cos φ (∂/∂r) e_x + cos φ cos θ /r (∂/∂ θ ) e_x - sinφ /ρ (∂/∂φ )e_x + sin θ sin φ (∂/∂r) e_y + sin φ cos θ /r (∂/∂ θ ) e_y + cos φ /r sin θ (∂/∂φ )e_y + cos θ (∂/∂r) e_z - sin θ /r (∂/∂ θ )e_z =

[sin θ cos φ e_x + sin θ sin φ e_y + cos θ e_z ](∂/∂r) + [cos φ cos θ /r e_x + sin φ cos θ /r e_y - sin θ /r e_z](∂/∂ θ ) + [- sinφ /ρ e_x + cos φ /r sin θ e_y ](∂/∂φ )

= [sin θ cos φ (sin θ cosφ er + cos θ cosφ e θ - sinφ eφ ) + sin θ sinφ (sin θ sinφ er + cos θ sinφ e θ + cosφ eφ ) + cos θ (cos θ er - sin θ e θ ) ](∂/∂r) + [cos φ cos θ /r (sin θ cosφ er + cos θ cosφ e θ - sinφ eφ ) + sin φ cos θ /r (sin θ sinφ er + cos θ sinφ e θ + cosφ eφ ) - sin θ /r (cos θ er - sin θ e θ )](∂/∂ θ ) + [- sinφ /ρ (sin θ cosφ er + cos θ cosφ e θ - sinφ eφ ) + cos φ /r sin θ (sin θ sinφ er + cos θ sinφ e θ + cosφ eφ ) ](∂/∂φ )

= [(sin θ cos φ sin θ cosφ + sin θ sin φ sin θ sinφ + cos θ cos θ )(∂/∂r) + (cos φ cos θ /r sin θ cosφ - sin φ cos θ /r sin θ sinφ + sin θ /r cos θ )(∂/∂ θ ) - sinφ /ρ sin θ cosφ + cos φ /r sin θ sin θ sinφ )(∂/∂φ )]e_r +[(sin θ cos φ cos θ cosφ + sin θ sin φ cos θ sinφ - cos θ sin θ )(∂/∂r) + (cosφ cos θ /r cos θ cosφ + cos θ sinφ /r cos θ sinφ + sin θ /r sin θ )(∂/∂ θ ) + (- sinφ /ρ cos θ cosφ + cos φ /r sin θ cos θ sinφ )(∂/∂φ )]e_θ + [(- cos φ sin θ /r sinφ + cosφ sin θ sin φ )(∂/∂r) + (- sinφ cos φ cos θ /r + cosφ sinφ cos θ /r)(∂/∂ θ ) + (sinφ sinφ /ρ + cosφ cos φ /r sin θ )(∂/∂φ )]e_φ

= [(∂/∂r)]e_r + [(1 /r )(∂/∂ θ )]e_θ + [(1/ρ )(∂/∂φ )]e_φ

∇ = [(∂/∂r)]e_r + [(1 /r )(∂/∂ θ )]e_θ + [(1/rsinθ )(∂/∂φ )]e_φ


8. The divergence in spherical coordinates:

Let: A = (A_r, A_θ, A_φ)

Now we will apply ∂/∂x on A_x , ∂/∂y on A_y and ∂/∂z on A_z and sum them:

∇ . A = ∂A_x/∂x + ∂A_y/∂y + ∂A_z/∂z

= sin θ cos φ (∂/∂r)[sin θ cosφ Ar + cos θ cosφ A θ - sinφ Aφ ] + cos φ cos θ /r(∂/∂ θ )[sin θ cosφ Ar + cos θ cosφ A θ - sinφ Aφ ] - sinφ /ρ(∂/∂φ )[sin θ cosφ Ar + cos θ cosφ A θ - sinφ Aφ ] + sin θ sin φ (∂/∂r)[sin θ sinφ Ar + cos θ sinφ A θ + cosφ Aφ ] + sin φ cos θ /r (∂/∂ θ )[sin θ sinφ Ar + cos θ sinφ A θ + cosφ Aφ ] + cos φ /r sin θ (∂/∂φ )[sin θ sinφ Ar + cos θ sinφ A θ + cosφ Aφ ] + cos θ (∂/∂r)[cos θ Ar - sin θ A θ ] - sin θ /r (∂/∂ θ )[cos θ Ar - sin θ A θ ]

= [sin² θ cos²φ + sin² θ sin²φ + cos² θ ] (∂Ar/∂r) + [cos²φ cos² θ /r + sin²φ /ρ + sin²φ cos² θ /r + sin θ cos²φ /ρ + sin² θ /r] Ar + [- cos²φ cos θ sinθ/r + cos θ sin²φ /ρ - sin²φcos θ sin θ /r + cos θ cos²φ /ρ + cos θ sin θ /r]A θ + cos²φ cos² θ /r + sin²φ cos² θ /r + sin² θ /r]∂A θ /∂θ + [sinφ cosφ /ρ - cosφ sinφ /ρ ]Aφ + [sin²φ /ρ + cos²φ /ρ]∂Aφ /∂φ

= (2/r) Ar + ∂Ar/∂r + cosφ /ρ A θ + (1/r)∂A θ /∂θ + (1/ρ)∂Aφ /∂φ

= (1/r²) ∂[r²A_r]/∂r + (1/r sinθ)&part[sinθA_θ]/∂θ + 1/r sinθ)∂[A_φ]/∂φ

∇ . A = (1/r²) ∂[r²A_r]/∂r + (1/r sinθ)∂[sinθA_θ]/∂θ +
1/r sinθ)∂[A_φ]/∂φ


9. The curl of a vector in spherical coordinates:

Let A = (A_r, A_θ, A_φ)

We can calculate Curl A this way:

Curl (A) = ∇ x A = e_x e_y e_z ∂/∂x ∂/∂y ∂/∂z A_x A_y A_z

= (∂[A_z]/∂y - ∂[A_y]/∂z)e_x + ∂[A_x]/∂z - ∂[A_z]/∂x) e_y + ∂[A_y]/∂x - ∂[A_x]/∂y) e_z And write all the related expressions. But its too long.

We will, instead use the DEL operator, which is:

∇ = [(∂/∂r)]er + [(1 /r )(∂/∂ θ )]e θ + [(1/rsin θ )(∂/∂φ )]eφ

er = sin θ cosφ ex + sin θ sinφ ey + cos θ ez
eθ = cos θ cosφ ex + cos θ sinφ ey - sin θ ez
eφ = - sinφ ex + cosφ ey

We will use:

∂er/∂r = 0	∂er/∂ θ = e θ	∂er/∂φ = sin θ eφ
∂e θ /∂r = 0	∂e θ /∂ θ = - er ∂e θ	∂φ = cos θ eφ
∂eφ /∂r = 0	∂eφ /∂ θ = 0	∂eφ /∂φ = - (sin θ er + cos θ e θ )
er x er = 0	e θ x e θ = 0	eφ x eφ = 0
er x e θ = eφ	eφ x er = e θ	e θ x eφ = er

Then:

Curl A = ∇ x A = [(∂/∂r) er + (1 /r )(∂/∂ θ ) e θ + (1/rsin θ )(∂/∂φ )eφ ] x [ Ar er + A θ e θ + Aφ eφ ] = [(∂/∂r) er + (1 /r )(∂/∂ θ ) e θ + (1/rsin θ )(∂/∂φ )eφ ] x [ Ar er + A θ e θ + Aφ eφ ]

= er x [(∂/∂r) Ar er + (∂/∂r) A θ e θ + (∂/∂r) Aφ eφ ] + (e θ /r) x [(∂/∂ θ )Ar er + (∂/∂ θ )A θ e θ + (∂/∂ θ )Aφ eφ ] + (1/rsin θ ) eφ x [(∂/∂φ )Ar er + (∂/∂φ )A θ e θ + (∂/∂φ )Aφ eφ ]

= (∂Ar /∂r) er x er + (∂A θ /∂r) er x e θ + (∂Aφ /∂r) er x eφ + Ar er x(∂er/∂r) + A θ er x(∂e θ /∂r) + Aφ er x(∂eφ /∂r) + (∂Ar/∂ θ )(e θ /r) x er + (∂A θ /∂ θ )(e θ /r) x e θ + (∂Aφ /∂ θ )(e θ /r) x eφ + Ar(e θ /r) x (∂er /∂ θ ) + A θ (e θ /r) x (∂e θ /∂ θ ) + Aφ (e θ /r) x (∂eφ /∂ θ ) + (1/rsin θ )(∂Ar/∂φ ) eφ x er + (1/rsin θ )(∂A θ /∂φ ) eφ x e θ + (1/rsin θ ) (∂Aφ /∂φ ) eφ x eφ Ar(1/rsin θ ) eφ x [(∂er/∂φ ) + A θ (1/rsin θ ) eφ x (∂e θ /∂φ ) + Aφ (1/rsin θ ) eφ x (∂eφ /∂φ )

= 0 + (∂A θ /∂r)eφ - (∂Aφ /∂r)e θ + 0 + 0 + 0 + - (∂Ar/∂ θ )(eφ /r) + 0 + (∂Aφ /∂ θ )(er /r)+ 0 + (1/r)A θ eφ + 0 + (1/rsin θ )(∂Ar/∂φ ) e θ - (1/rsin θ )(∂A θ /∂φ ) er + 0 0 + 0 - Aφ (1/rsin θ ) (sin θ e θ - cos θ er) ]

= (1/r)(∂Aφ /∂ θ ) er - (1/rsin θ )(∂A θ /∂φ ) er + Aφ ( cos θ /rsin θ ) er + (1/rsin θ )(∂Ar/∂φ ) e θ - Aφ (sin θ /rsin θ ) e θ - (∂Aφ /∂r)e θ + (1/r)A θ eφ + (∂A θ /∂r)eφ - (1/r)(∂Ar/∂ θ ) eφ


A = (Ar, A θ , Aφ )

∇ x A = [(1/r)(∂Aφ /∂ θ ) - (1/rsin θ )(∂A θ /∂φ ) + Aφ (cos θ /rsin θ )] er + [ (1/rsin θ )(∂Ar/∂φ ) - (1/r)Aφ - (∂Aφ /∂r)] e θ + [(1/r) A θ + (∂A θ /∂r) - (1/r)(∂Ar/∂ θ )]eφ

Or:

∇ x A = (1/rsin θ )[(∂(sin θ A_φ )/∂ θ ) - (∂A _θ /∂φ )] e_r + (1/rsin θ )[(∂A_r/∂φ ) - sin θ (∂(r A_φ )/∂r)] e _θ + (1/r)[∂(r A _θ )/∂r - ∂A_r/∂ θ ]e_φ