Calculus III
Contents
3 Dimensional space
Partial derivatives
Multiple integrals
Vector Functions
Line integrals
Surface integrals
Vector operators
Applications
© The scientific sentence. 2010
|
|
Calculus III:
Surface area
Surface area element
We are going to determine between dS and dA.
Ds is rhe surface element , and dA is the surface area element.
1. Surface area element
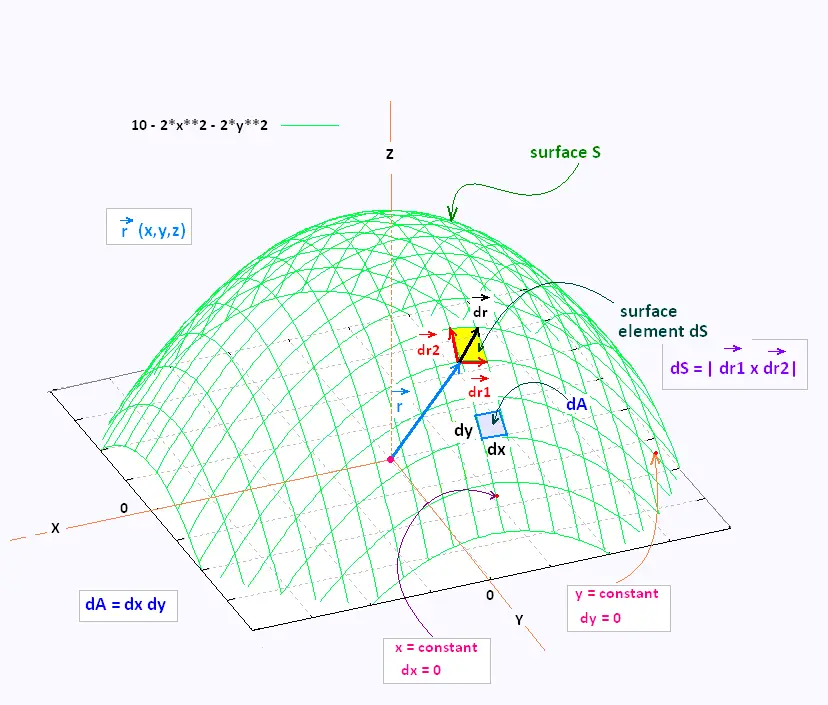
The vector position  points
on the surface S.
=
x  +
y  +
z 
Its derivative is:
 =
dx +
dy +
dz
z = f(x,y) → dz = (∂f/∂x)dx + (∂f/∂y))dy
=  +
 .
= (y = const) = dx +
dz
=
dx +
((∂f/∂x)dx + (∂f/∂y)dy
)
=
dx ( + (∂f/∂x))
Similarly, in the y direction, dx = 0, which leads to:
=
dy ( + (∂f/∂y))
Now, let's evaluate dS:
| dS = | x | = |
 |
|
|
|
|
| dx
|
0
|
dx fx
|
| 0
|
dy
|
dy fy
|
= - dx dy (∂f/∂x)
- dx dy (∂f/∂y) +
dx dy
Taking its magnitude:
dS = | x | =
= |- dx dy (∂f/∂x)
- dx dy (∂f/∂y) +
dx dy | =
√{[dx dy (∂f/∂x)]2 +
[dx dy (∂f/∂y)]2 +
[dx dy]2} =
dx dy √[(∂f/∂x)2 +
(∂f/∂y)2 +
1] =
dS = √[(∂f/∂x)2 +
(∂f/∂y)2 +
1] dx dy
=
dS = √(fx2 +
fy2 + 1) dx dy
dS = √(fx2 +
fy2 + 1) dx dy
2. Surface area element formula
To integrate a function f(x,y) over a surface S, we project the surface S on the xy-plane to get the corresponding region D, of area element dA = dx dy, where to integrate this function.
∫∫S f(x,y) dS = ∫∫D f(x,y) √(fx2 +
fy2 + 1) dA.
dS changes according to the formula:
|
|